Amazing AlgorithmsFor Solving Problems in SoftwareBarry S. StahlPrincipal Engineer - AZNerds.net@bsstahl@cognitiveinheritance.comhttps://CognitiveInheritance.com |

|
Favorite Physicists & Mathematicians
Favorite Physicists
Other notables: Stephen Hawking, Edwin Hubble, Leonard Susskind, Christiaan Huygens |
Favorite Mathematicians
Other notables: Daphne Koller, Grady Booch, Leonardo Fibonacci, Evelyn Berezin, Benoit Mandelbrot |
Fediverse Supporter
|

|
Some OSS Projects I Run
- Liquid Victor : Media tracking and aggregation [used to assemble this presentation]
- Prehensile Pony-Tail : A static site generator built in c#
- TestHelperExtensions : A set of extension methods helpful when building unit tests
- Conference Scheduler : A conference schedule optimizer
- IntentBot : A microservices framework for creating conversational bots on top of Bot Framework
- LiquidNun : Library of abstractions and implementations for loosely-coupled applications
- Toastmasters Agenda : A c# library and website for generating agenda's for Toastmasters meetings
- ProtoBuf Data Mapper : A c# library for mapping and transforming ProtoBuf messages
http://GiveCamp.org

Achievement Unlocked

Agenda
- 08:00 - 08:15 : Intro and Modeling
- 08:15 - 08:45 : Dynamic Programming
- 08:45 - 09:15 : Genetic Algorithms
- 09:15 - 09:45 : K-Means Clustering
- 09:45 - 10:00 : Break
- 10:00 - 10:15 : Clustering Wrap-up
- 10:15 - 10:45 : Best-Path Algorithms
- 10:45 - 11:15 : Cost-Minimization Algorithms
- 11:15 - 11:45 : Training Neural Networks
- 11:45 - 12:00 : Q&A and Wrap-up
- Bonus (if time allows) : LP & MIP
Simulates A Rational Actor
|

|
Models are the Blueprint
|
The success of a problem-solving algorithm is often determined before the algorithm even runs -- by how the problem is modeled |

|
Modeling
|
|
|
Workshop Goals
|

|
Knapsack Problems
|

|
Memoization
|

|
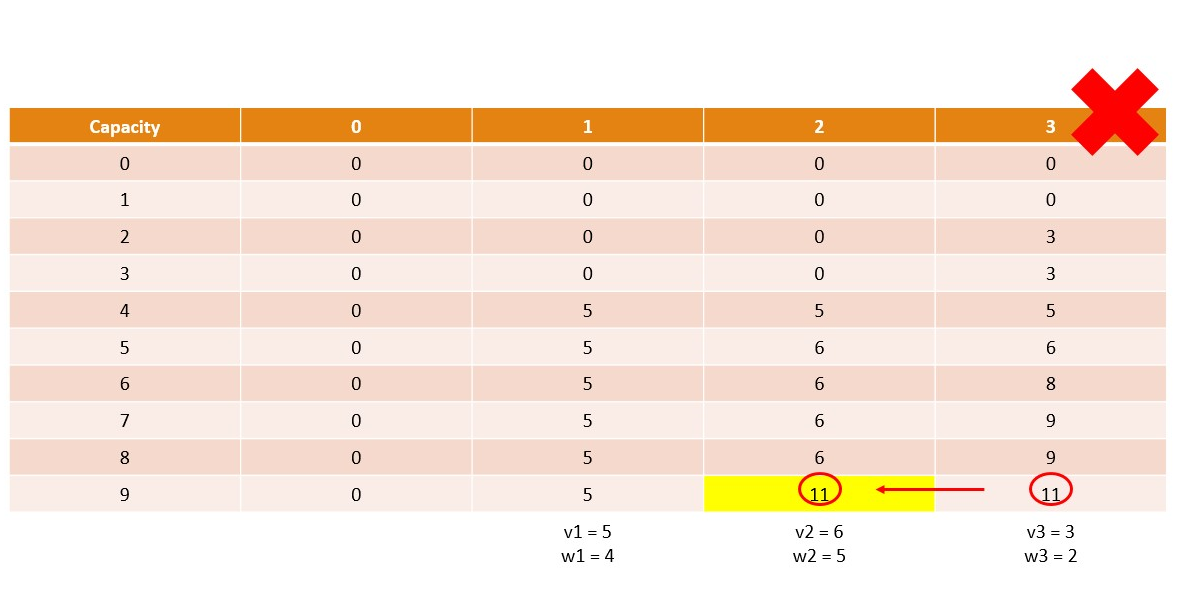
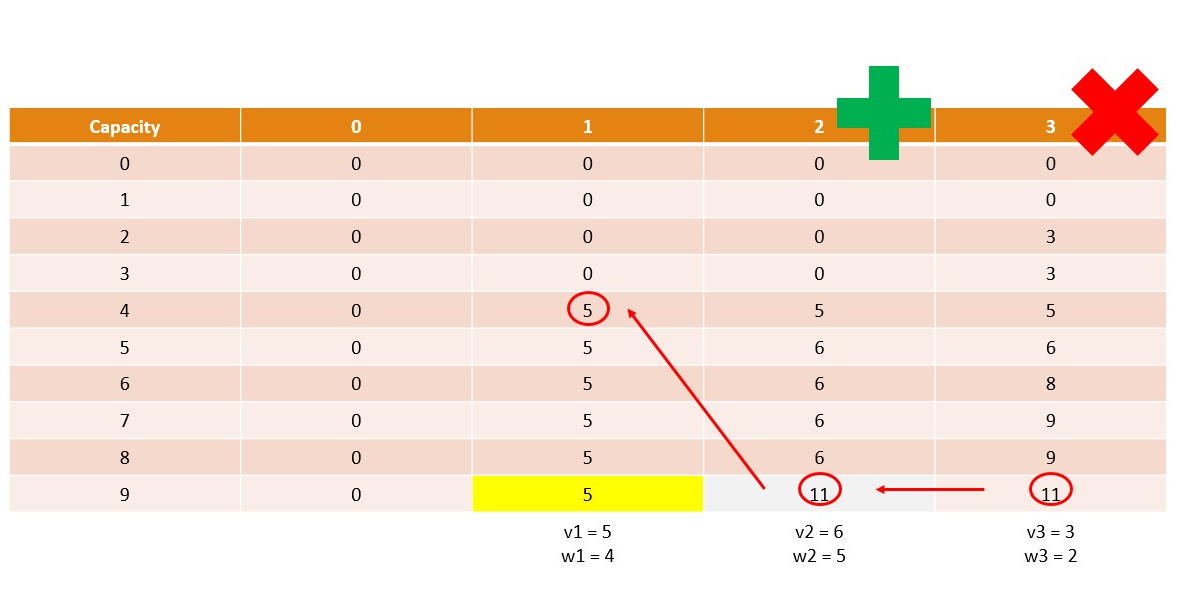
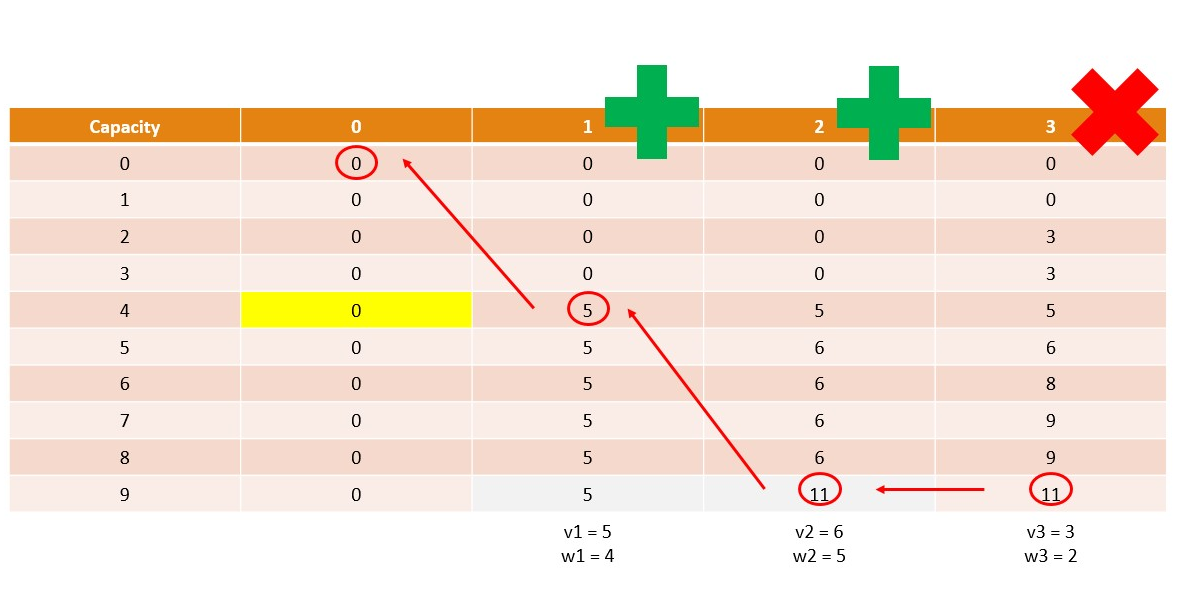
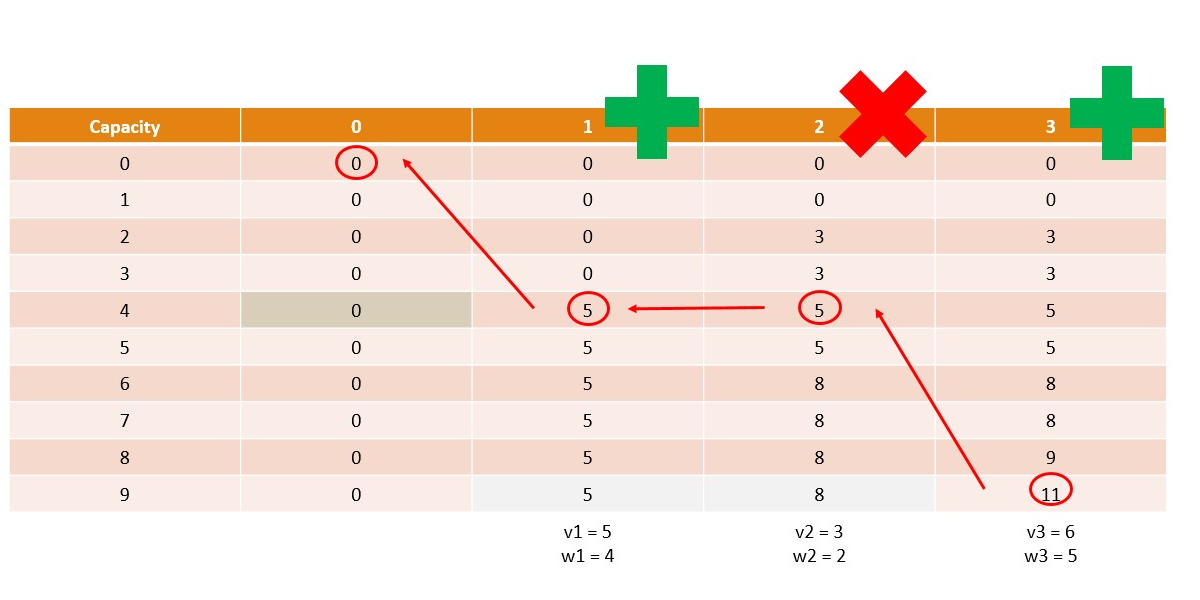
Canonical Knapsack Problem
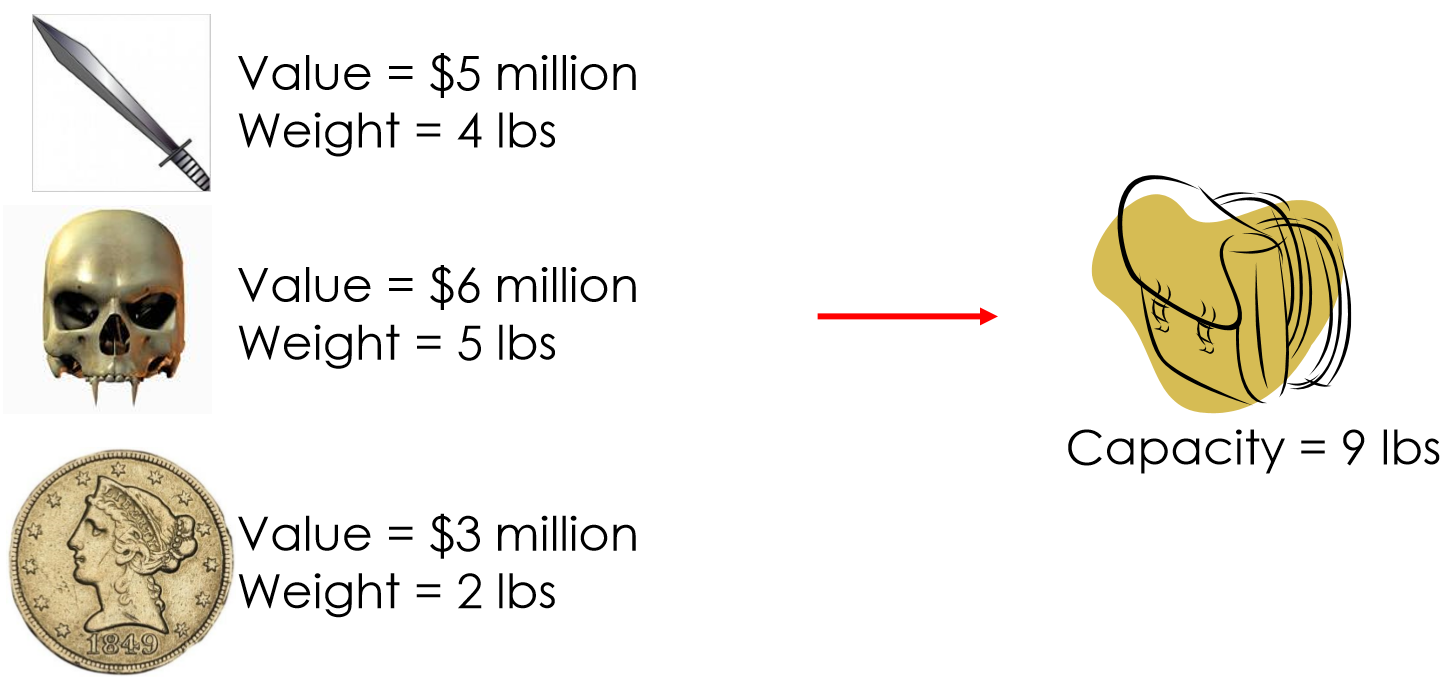
Memoization
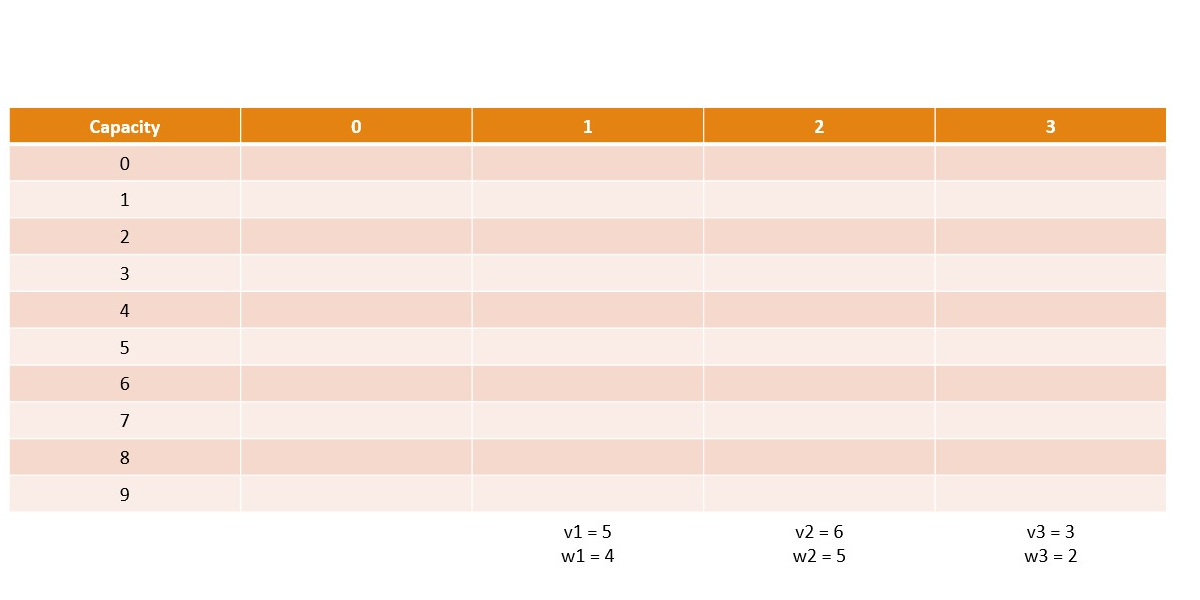
Memoization
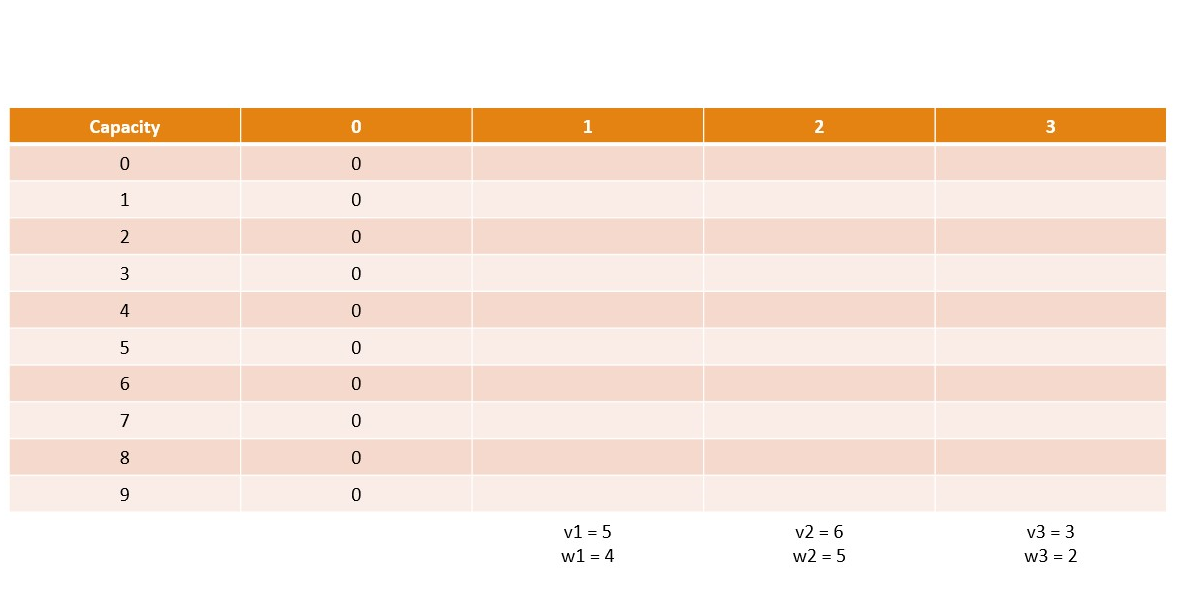
Memoization
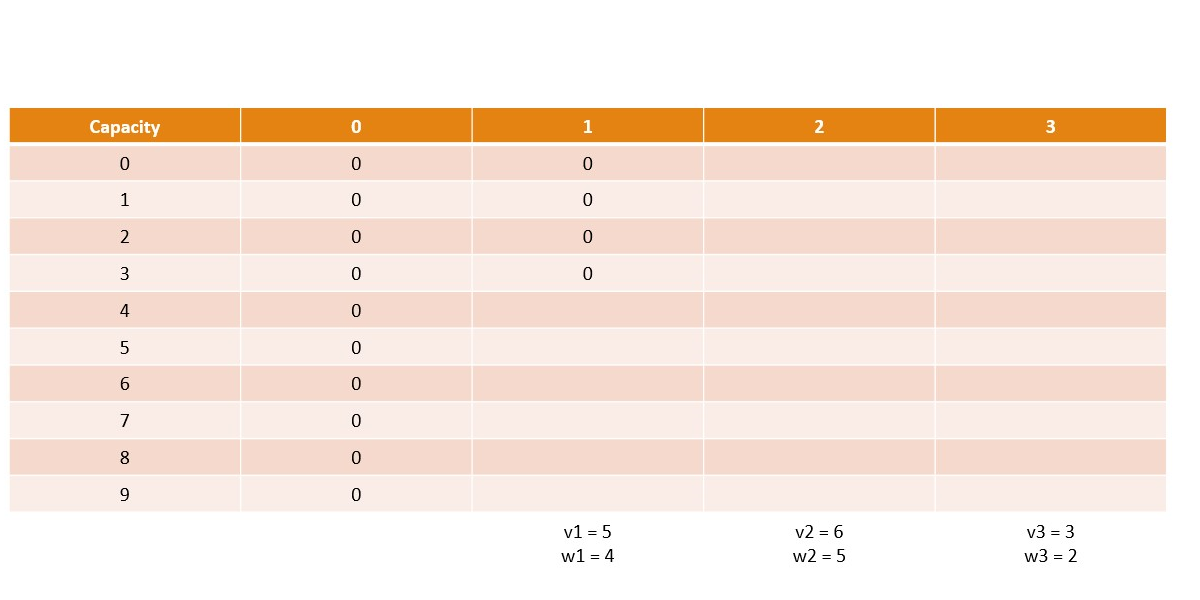
Memoization
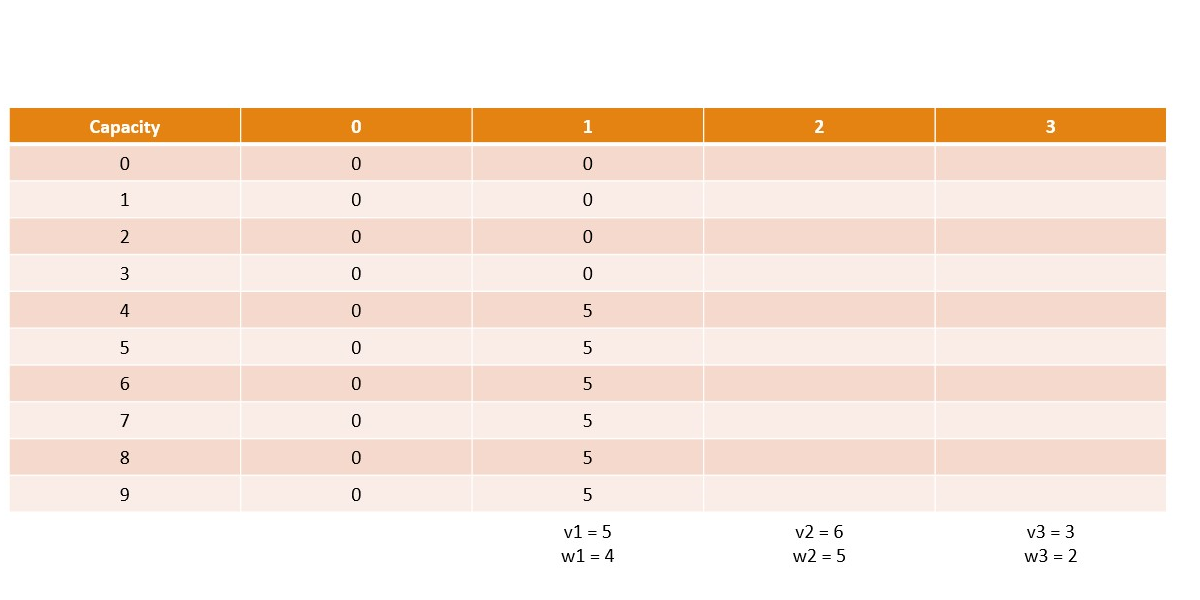
Memoization
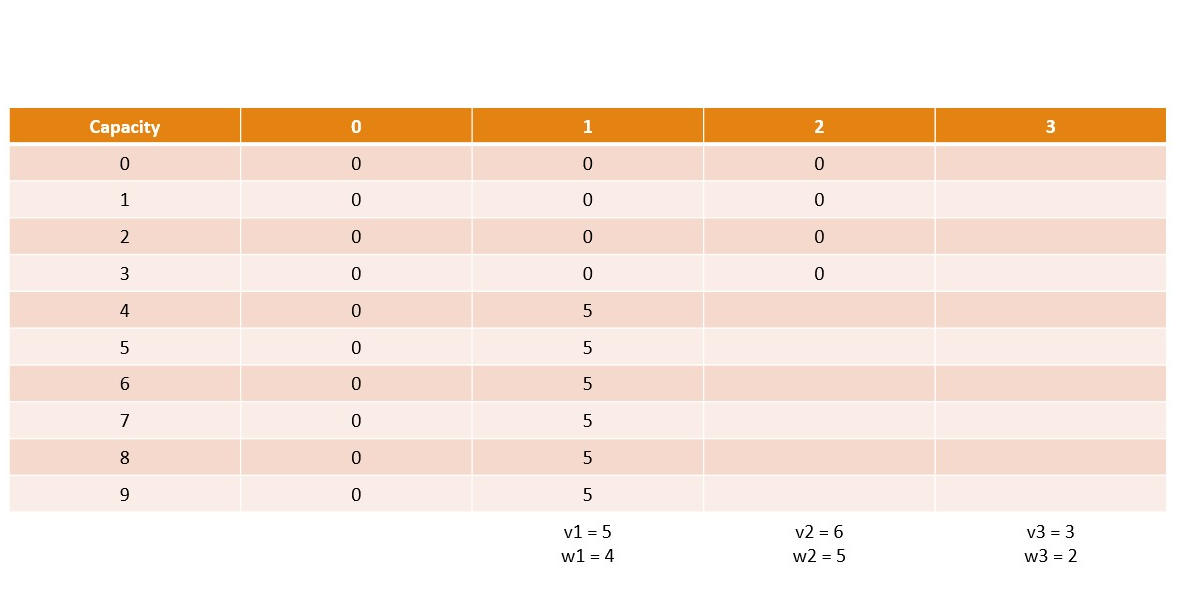
Memoization
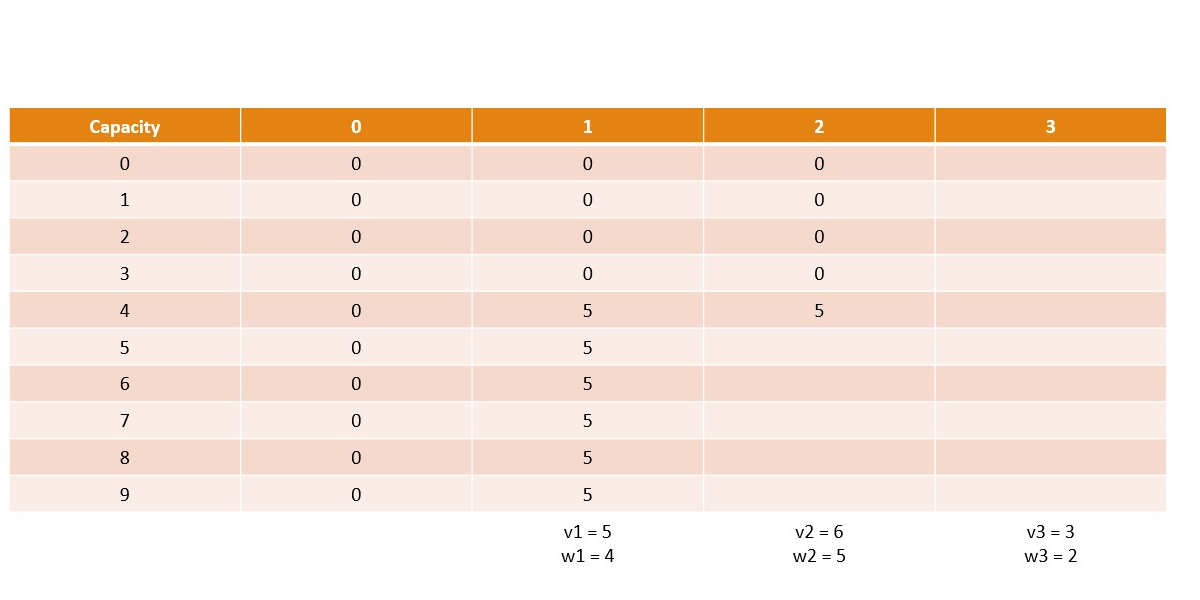
Memoization
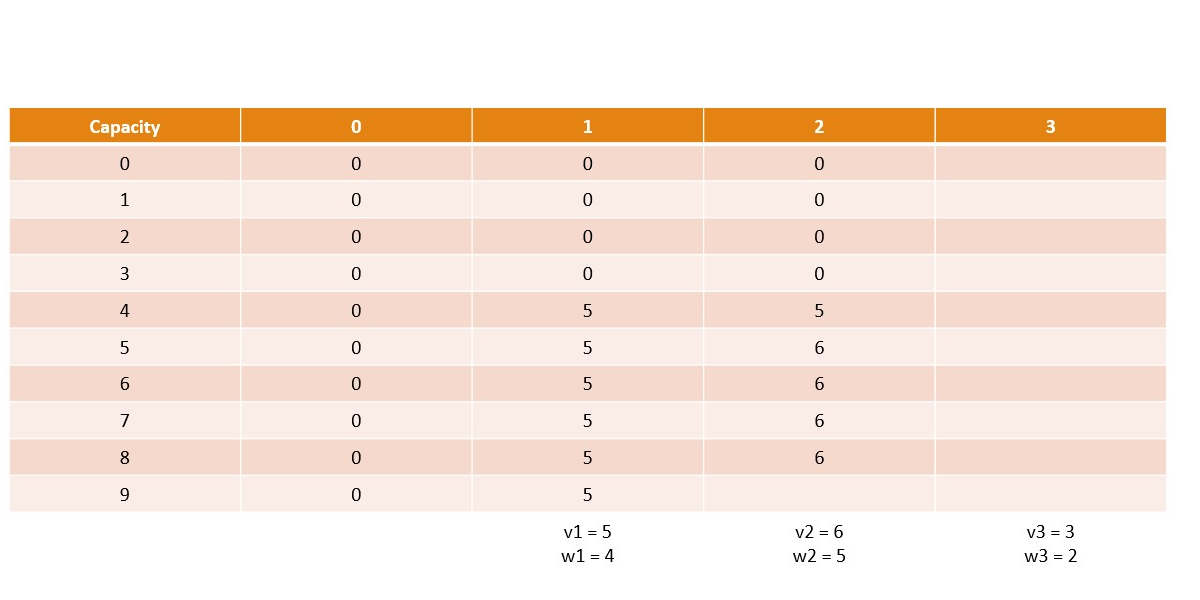
Memoization
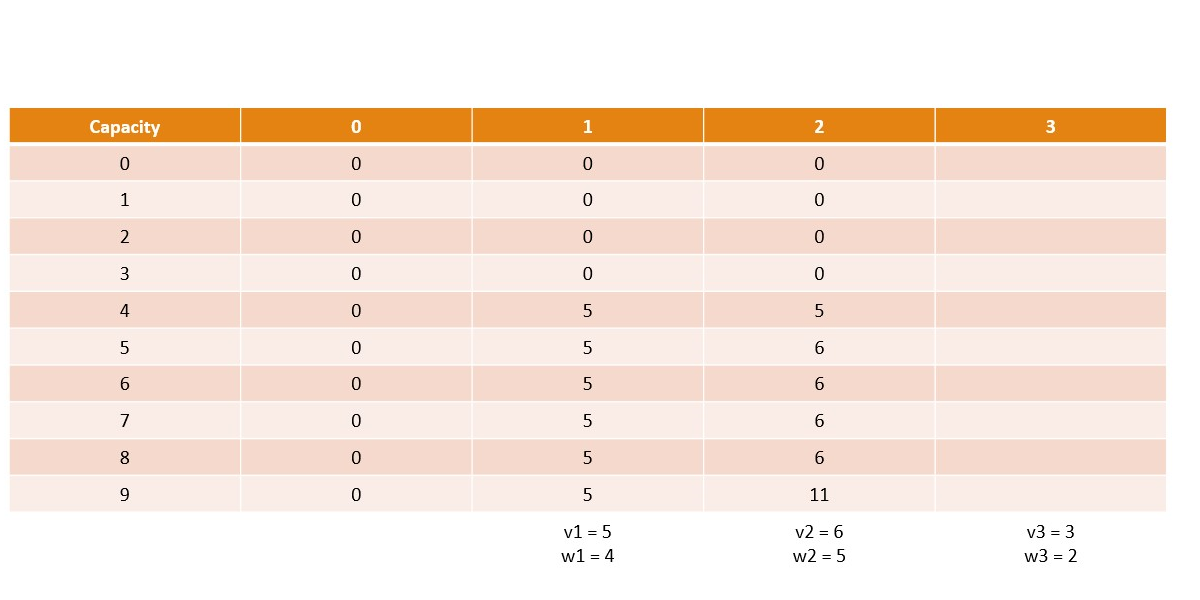
Memoization
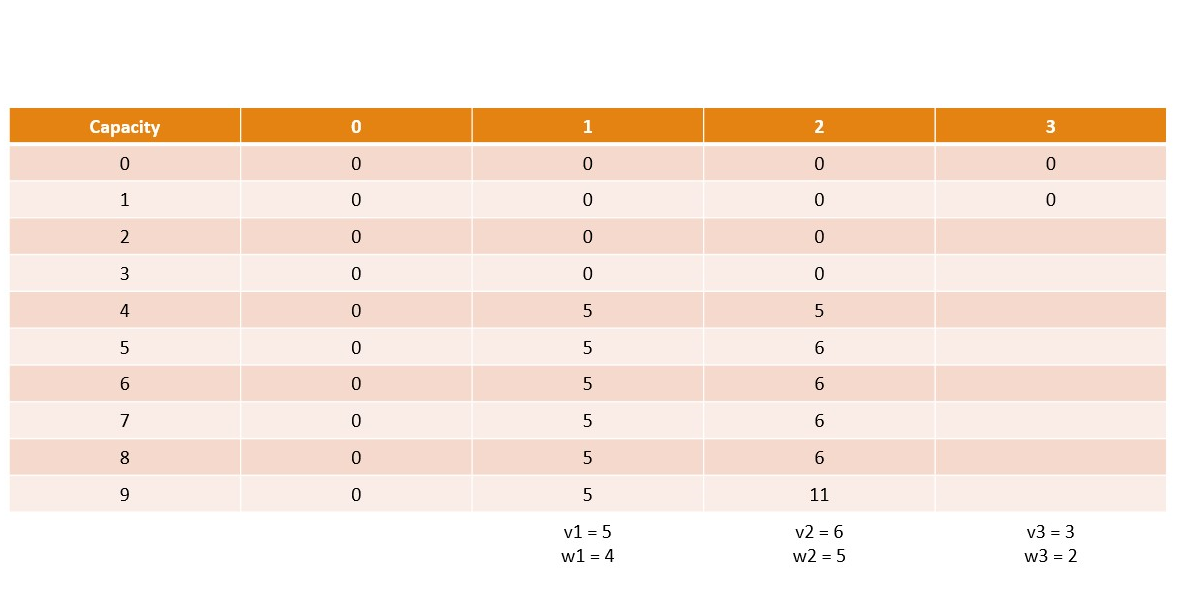
Memoization
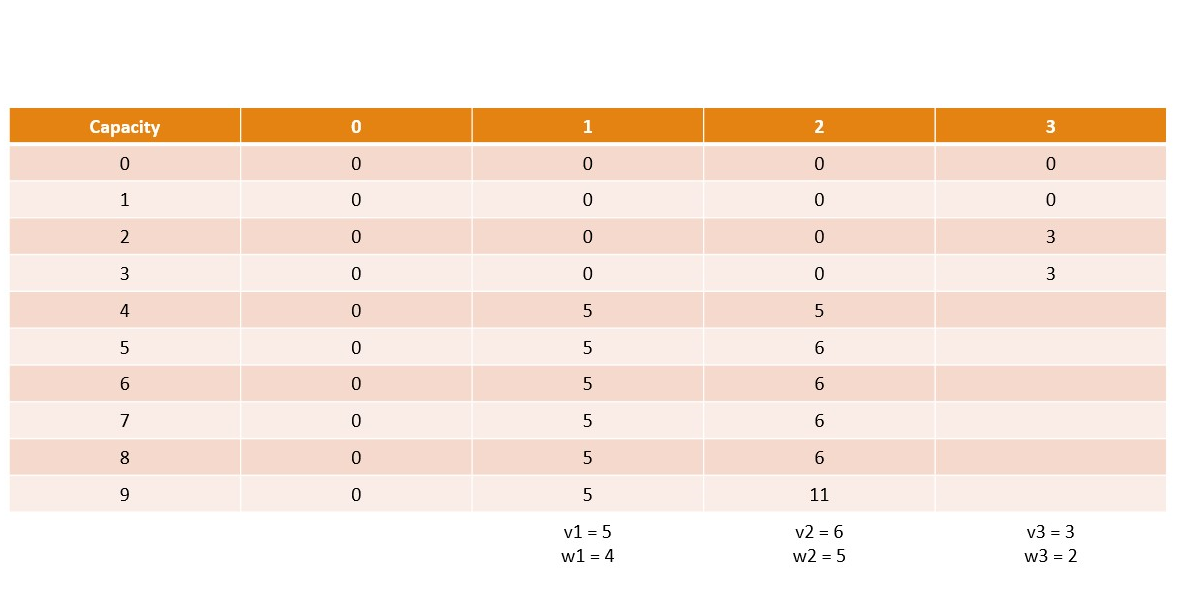
Memoization
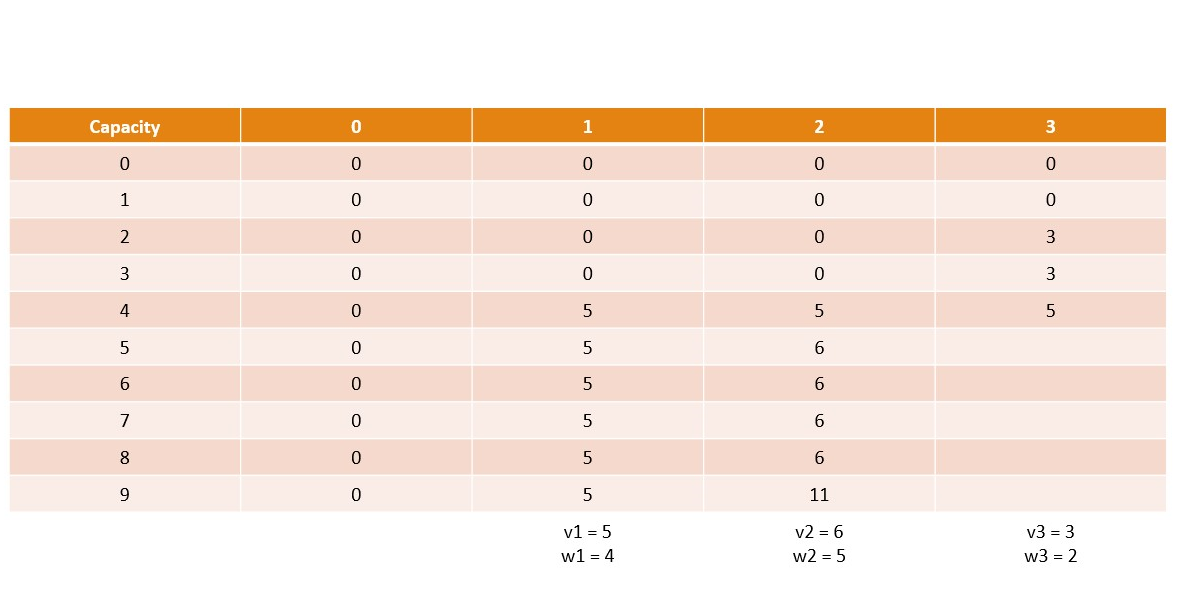
Memoization
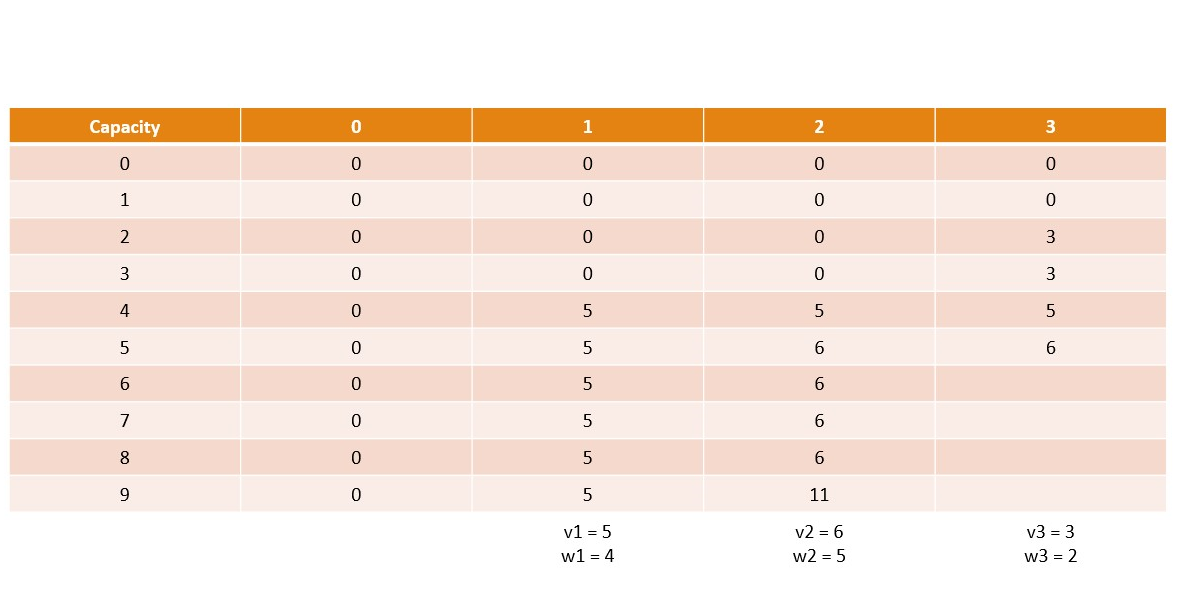
Memoization
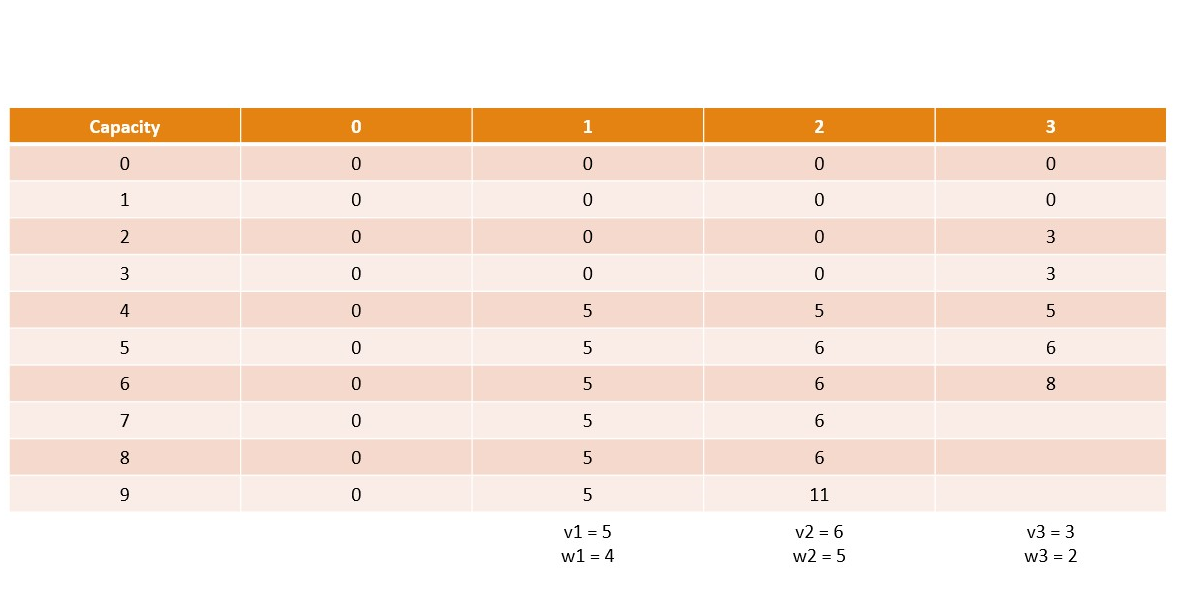
Memoization
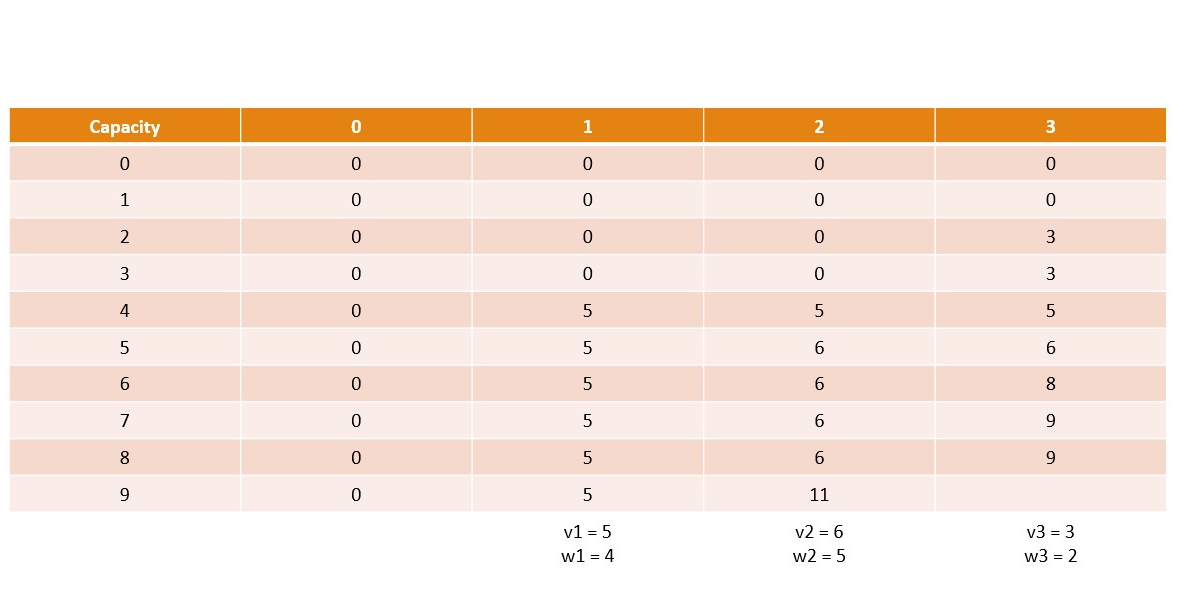
Memoization
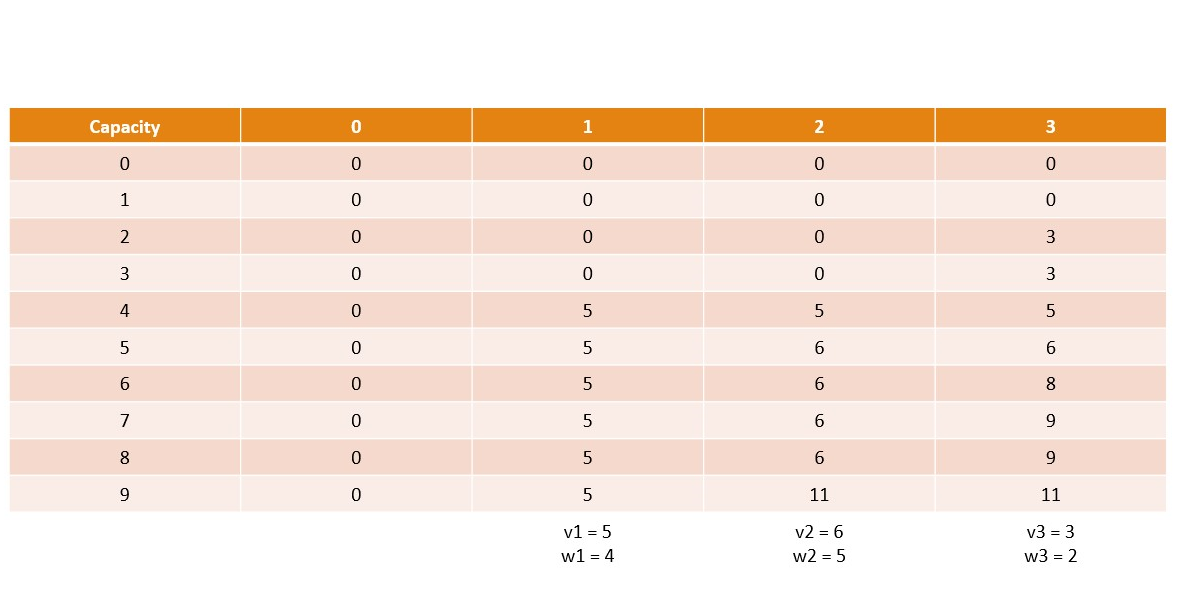
Memoization
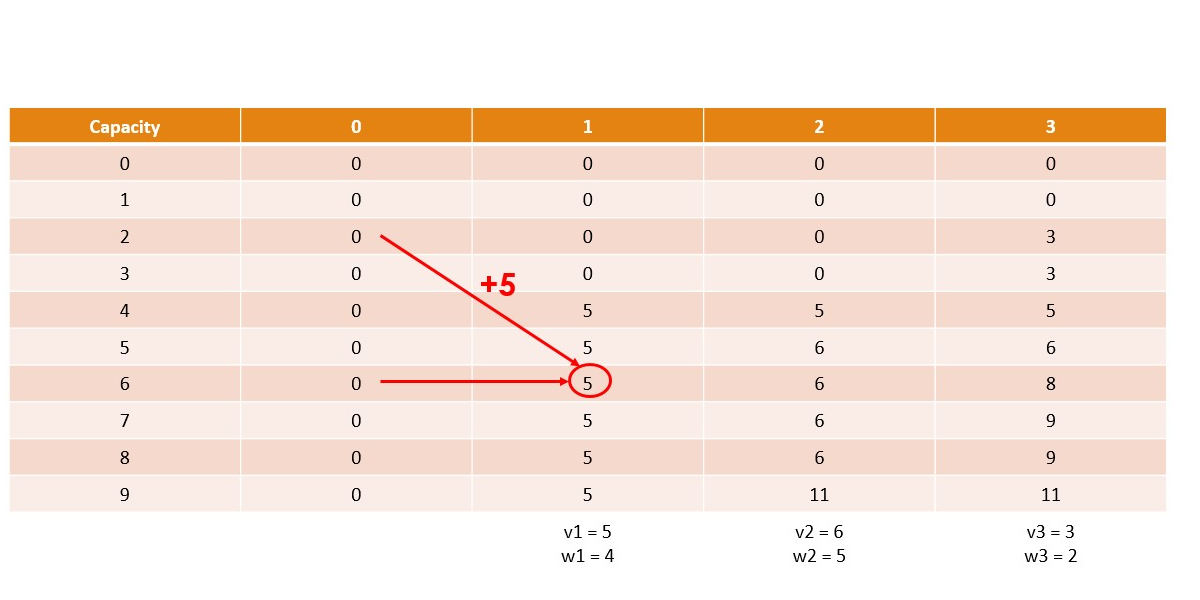
Memoization
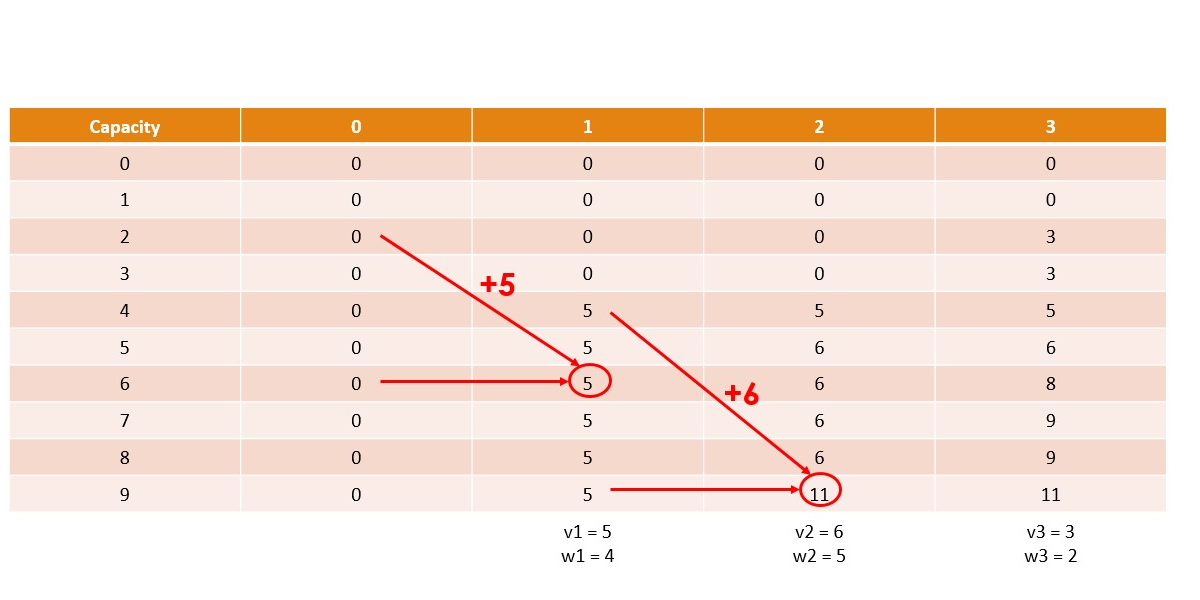
Memoization
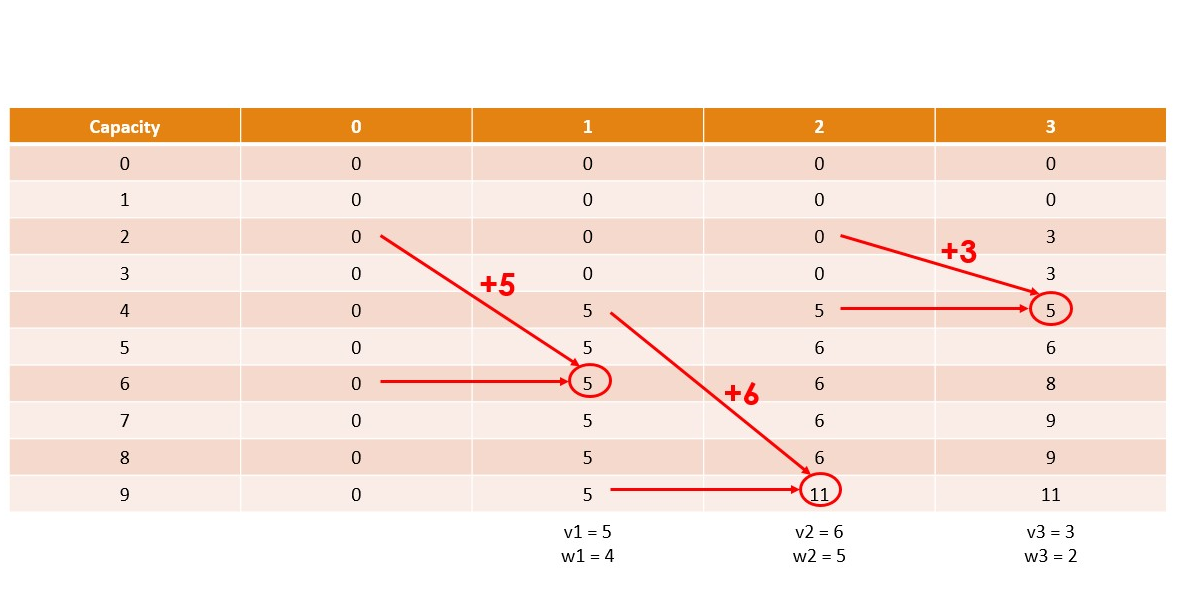
Memoization
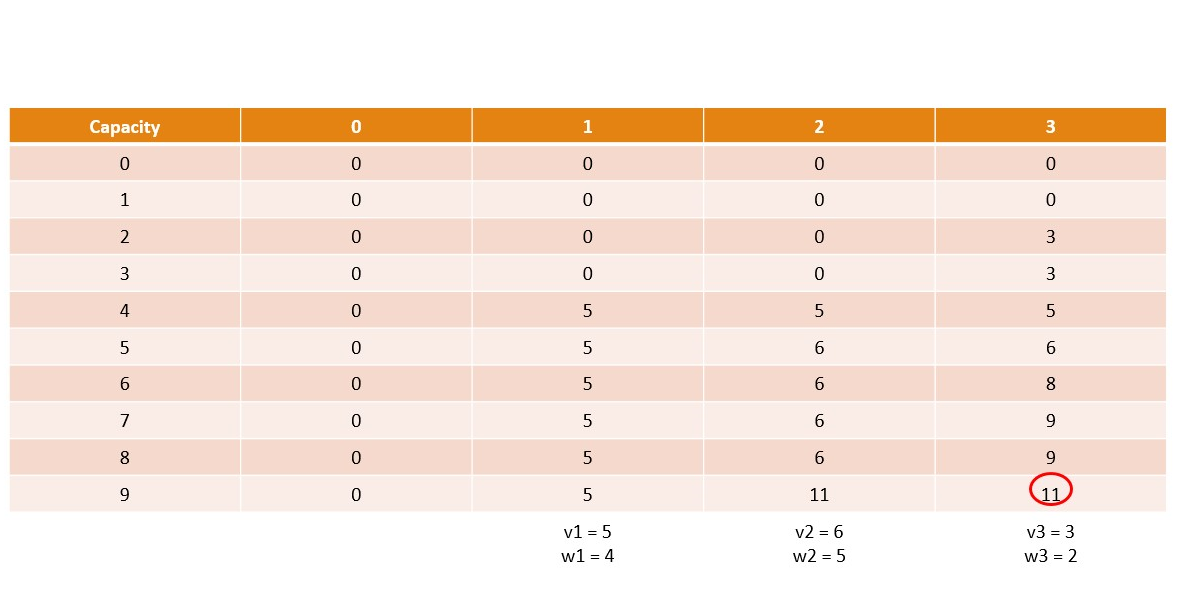
Memoization
Memoization
Memoization
Memoization
Dynamic Programming
A mathematical optimization technique
- Best for solving problems that can be described recursively
- Breaks the problem into smaller sub-problems
- Solves each small problem only once
- Guarantees an optimal solution
Optimization Problems
- Find the best values for a set of decision variables that
- Satisfies all constraints
- Maximizes the features we want
- Minimizes the features we don’t want
Simple Example - Chutes and Ladders
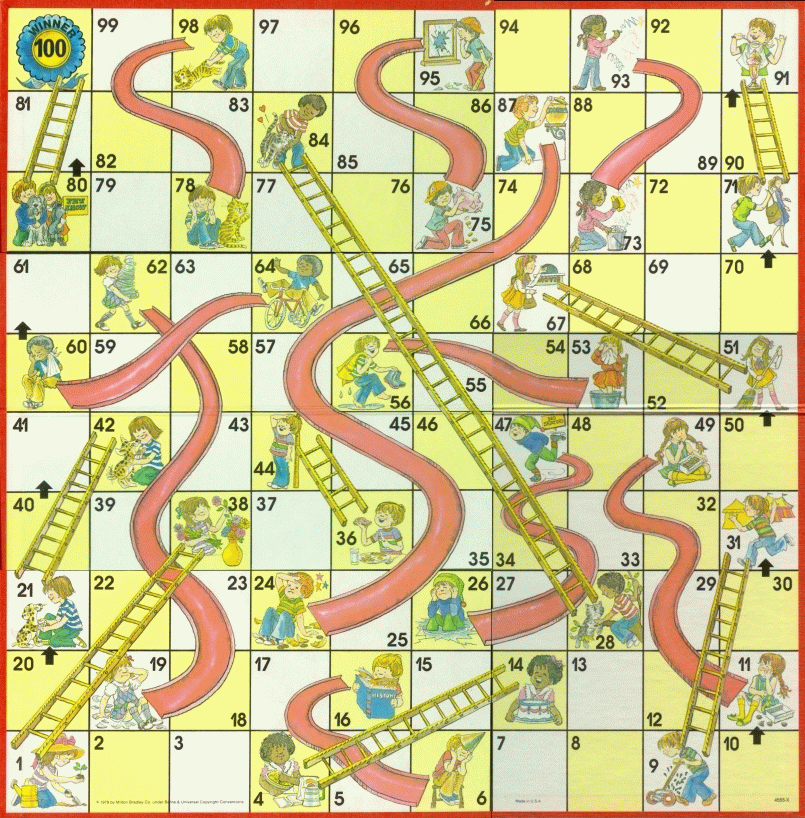
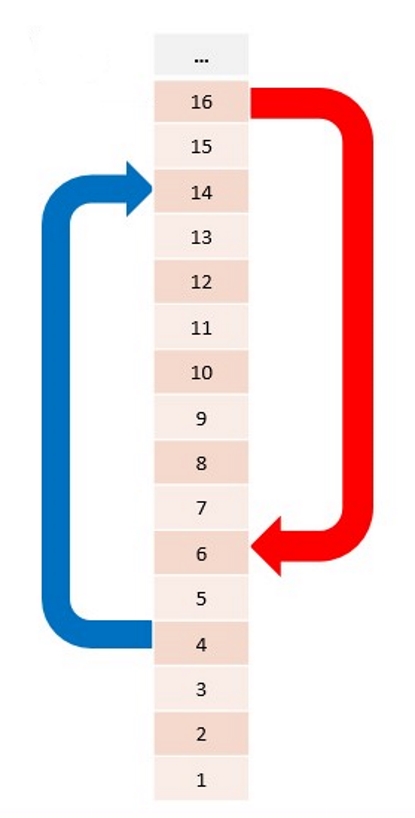
Chutes and Ladders - Greedy Algorithm
|
|
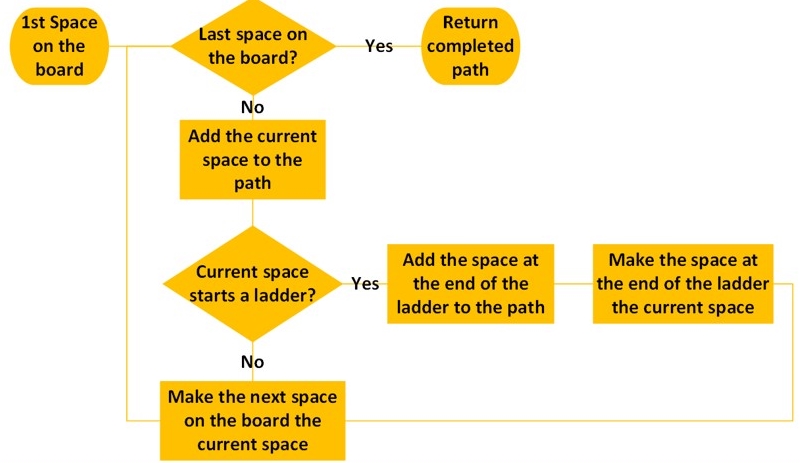
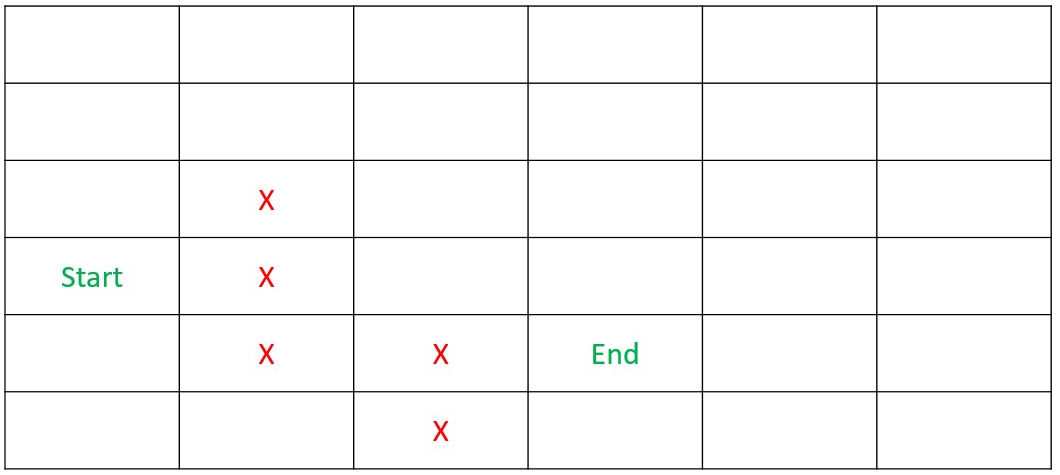
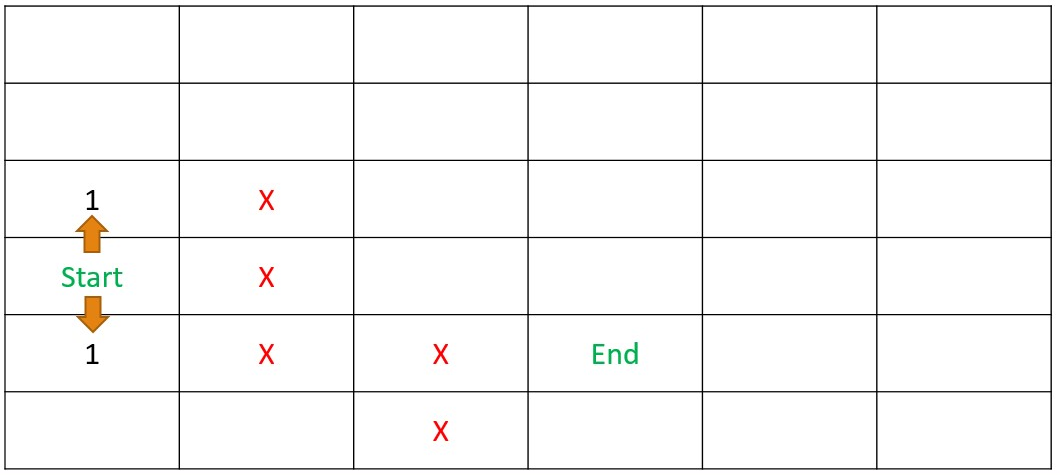
Dynamic Programming - Step 1
DetermineDistance(s,d)
|
|
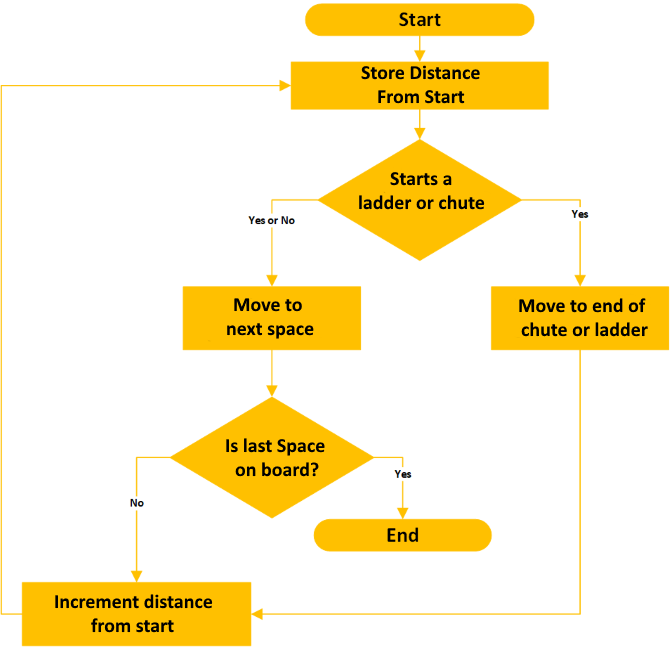
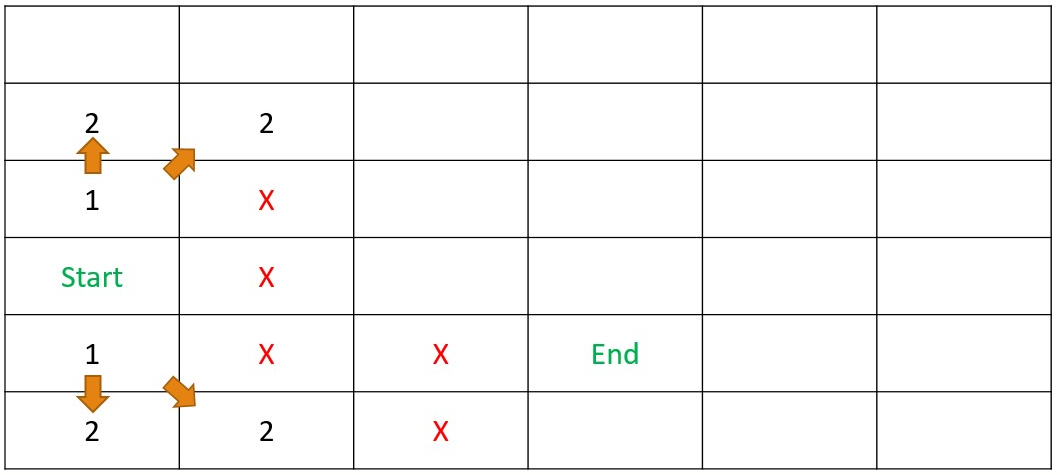
Dynamic Programming - Step 2
|
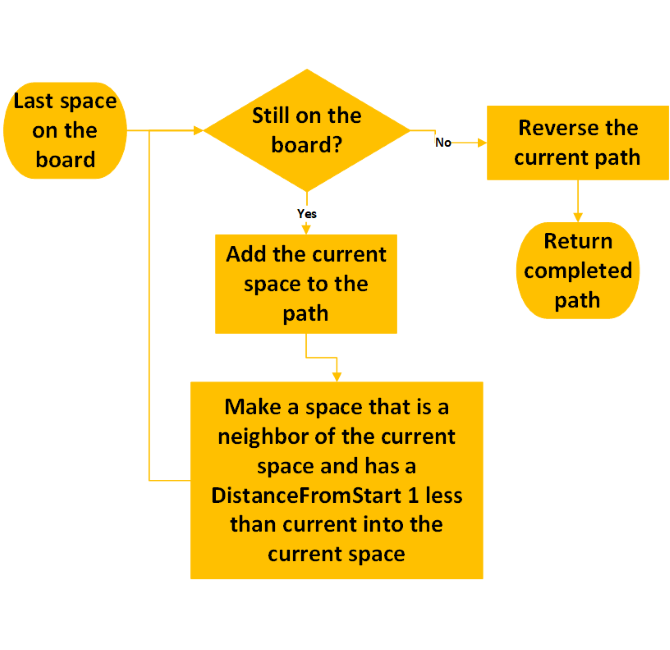
|
Memoization
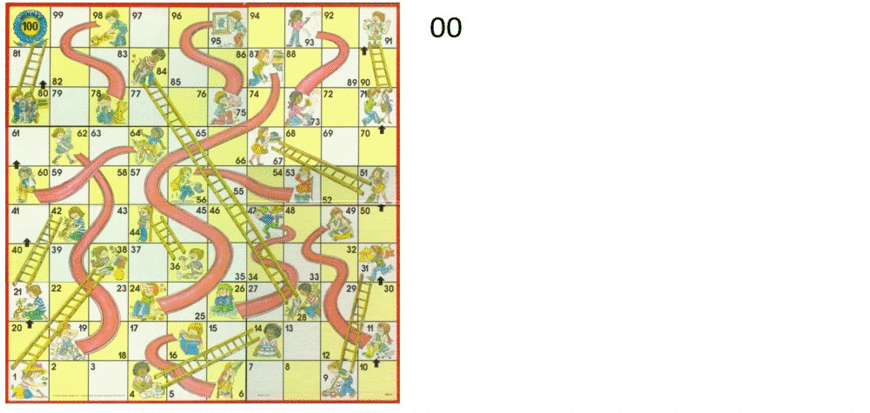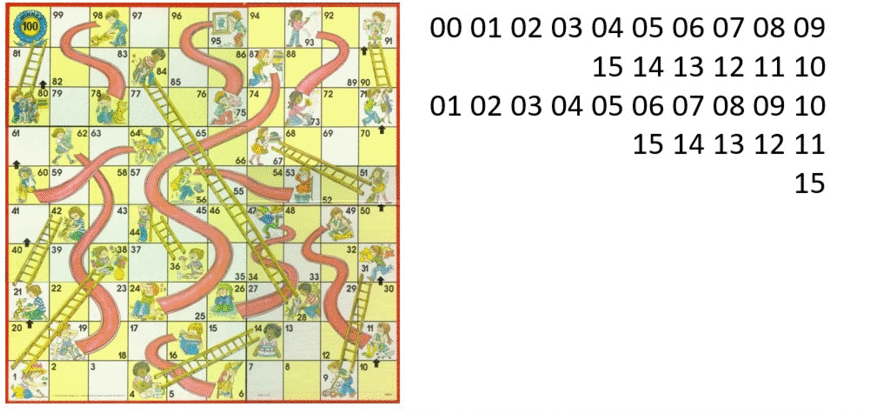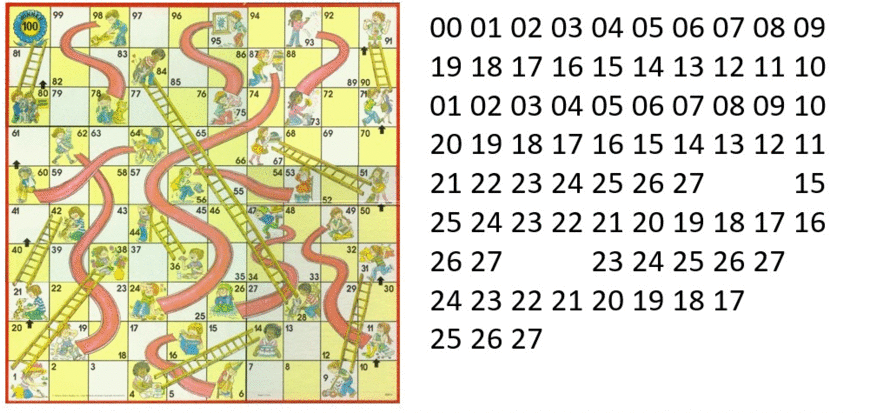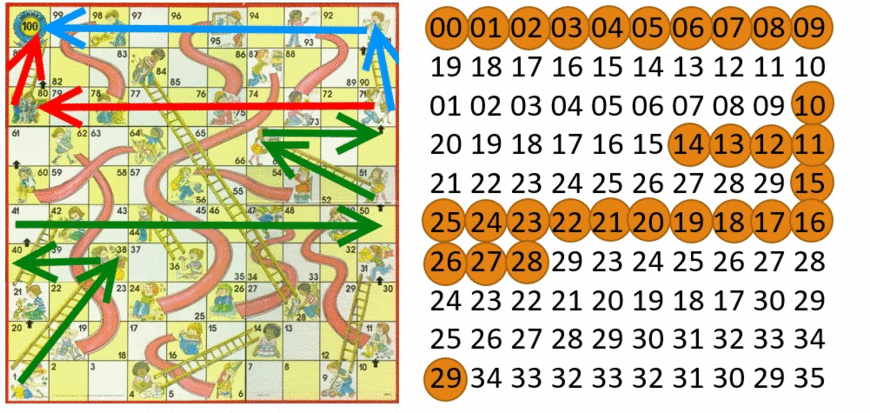
Shortest Path
Shortest Path
Shortest Path
Shortest Path
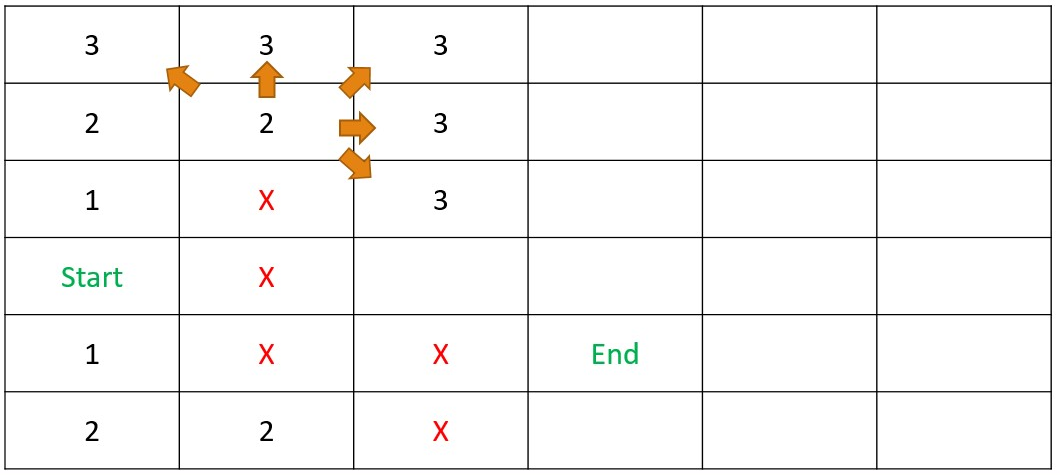
Shortest Path
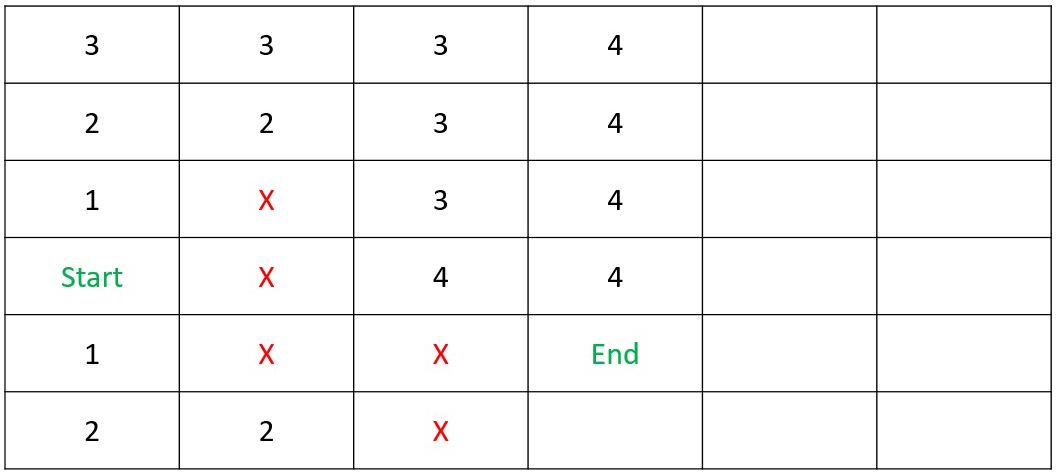
Shortest Path
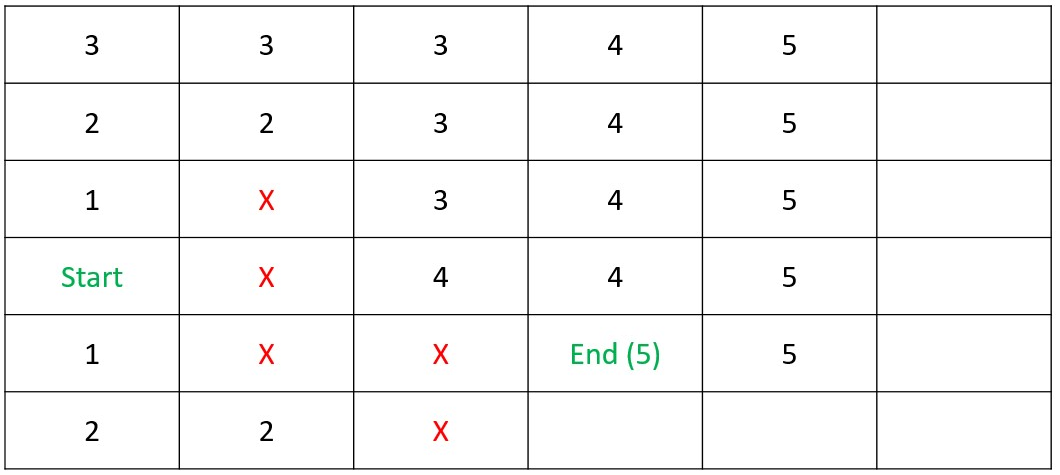
Shortest Path
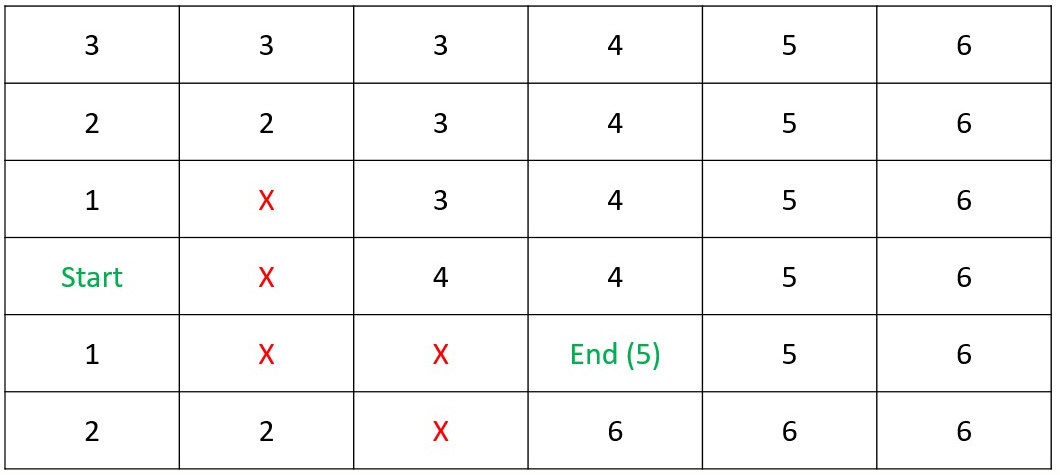
Shortest Path
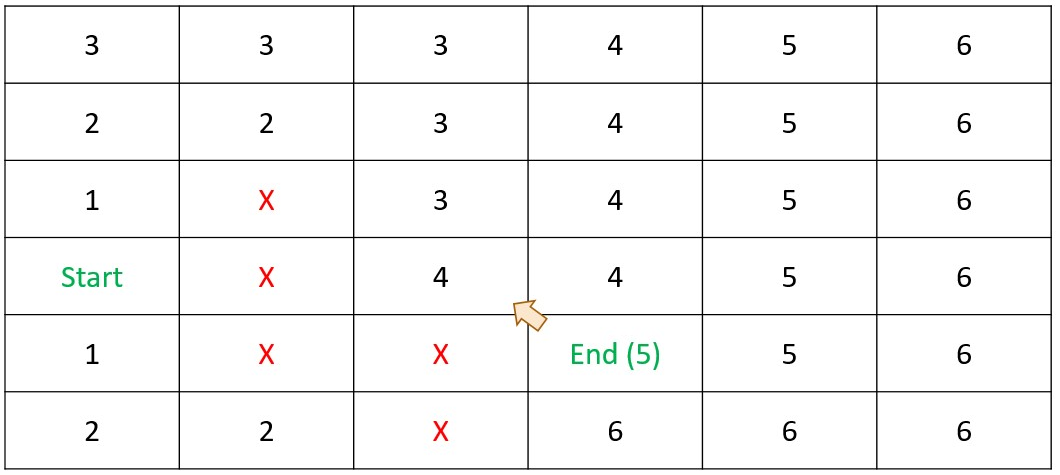
Shortest Path
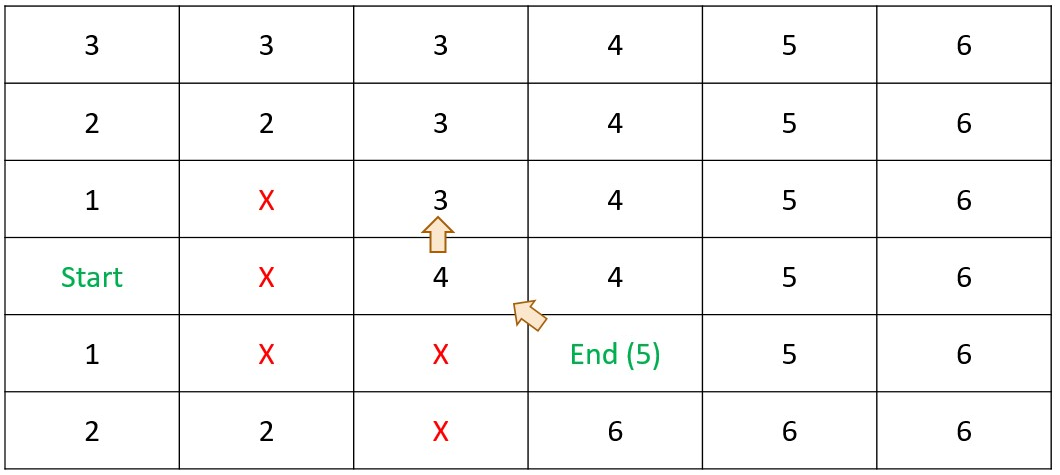
Shortest Path
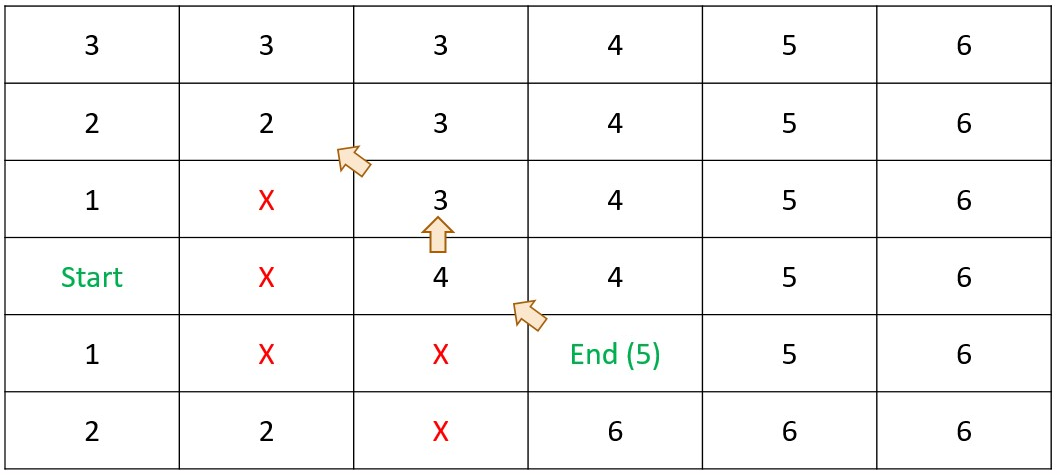
Shortest Path
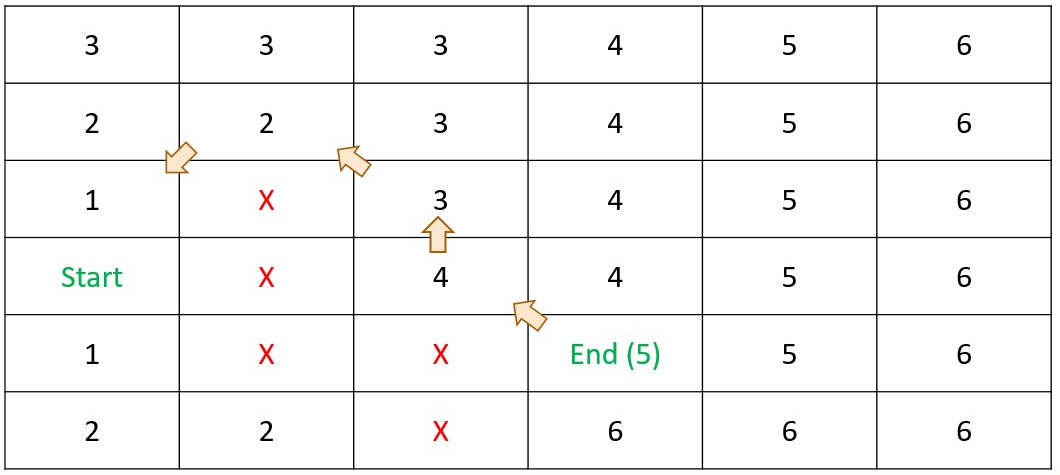
Shortest Path
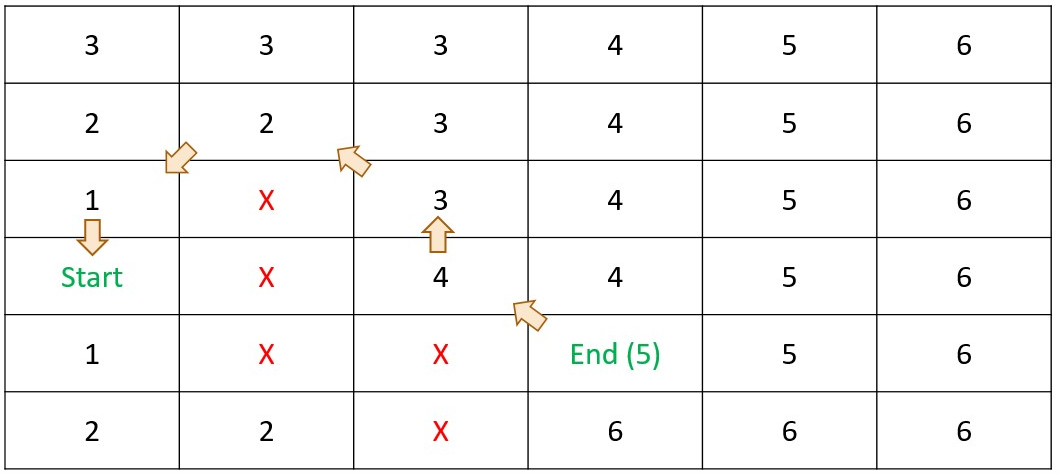
Summary - Dynamic Programming
- Populate the cache
- Simple calculations
- Build from the ground-up
- Use the cached data to determine the answer(s)
- Work backwards through the cache
- Guaranteed Optimality
- A fully populated cache means all options are explored
- Works in any number of dimensions
- Works with any graph (nodes & edges)
- Works best when
- Problems can be described recursively
- 1 or more axis are limited in scope
- Works best when
Use Case: Game Strategy
Find the best strategy in a multi-player board game
|

|
Other Model Types
|
|
|
Genetic Algorithms
Find Solutions by Simulating Darwinian Evolution
- Each candidate solution is defined by its properties (chromosomes)
- A fitness function is used to determine which solutions "survive"
- A simulation may be used as the fitness function
- Surviving solutions may mutate and evolve other solutions
Optimality is Never Guaranteed
- Optimal solution may never be found
- i.e. If a optimality requires a large combination of elements
- Optimum may be found but not recognized
- If conditions make that solution non-optimal at that moment
- i.e. If a key feature is not used during the simulation
- Minimize the liklihood by increasing simulation size
- If conditions make that solution non-optimal at that moment
Determine Our Game Strategy
|

|
Step 1 - Define DNA
A chromosome represents all of the possible decisions that can be made
Each gene represents a decision
- Ideally a gene fully describes a single game state
- If no decision is possible for a state, there is no gene for that state
An allele is an option for that decision
- If there are 3 options for a given state there will be 3 possible alleles for that gene
DNA of Chutes & Ladders
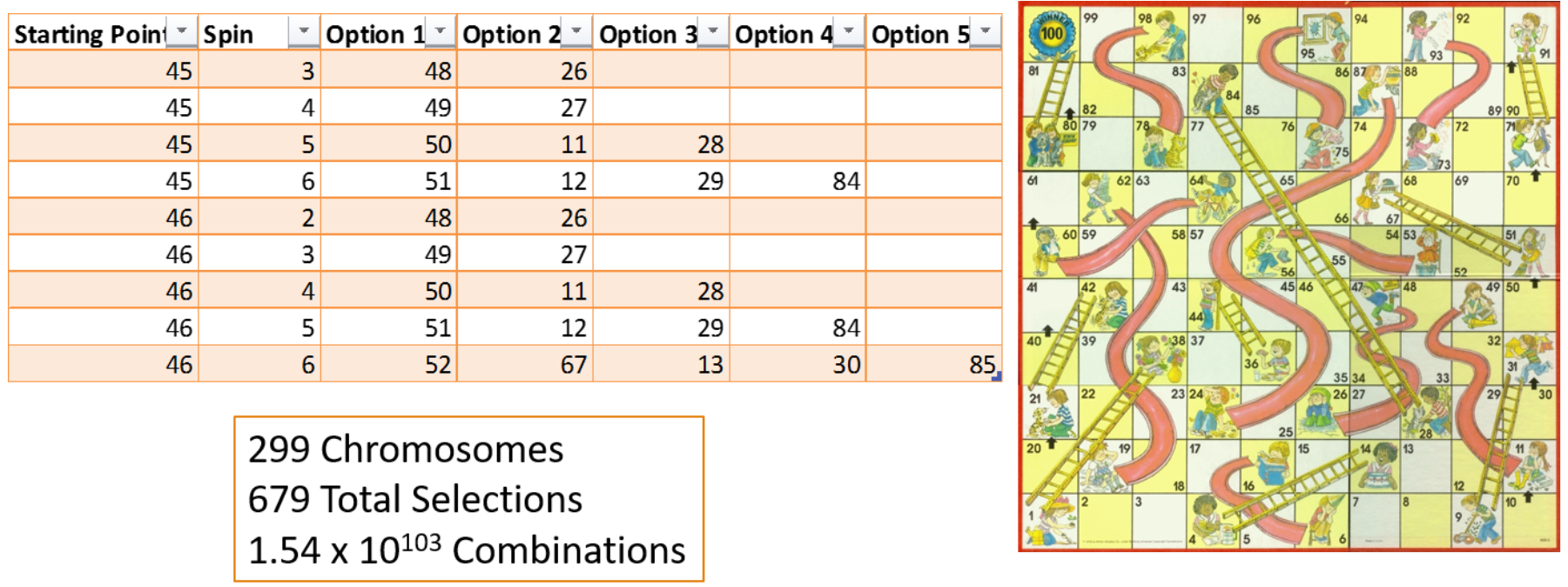
Step 2 - Setup Parameters
|
|
|
|
Genetic Algorithm
Step 3 - Run the Simulations
Options for Experimentation
Implement in your preferred language
- C# implementation is on GitHub
Augment to include what place the player is in
- i.e. Might make different decisions if started 1st vs 6th
Augment to include opponent locations
- i.e. Might make different decisions if opponents are close to the end
Define the DNA of another game
- Recommendation - stick with simpler games to start
- Avoid games like chess with massive complexity
Problem 2 - Semantic Distance

Embeddings
|

|
3-D Space Projected into 2-D
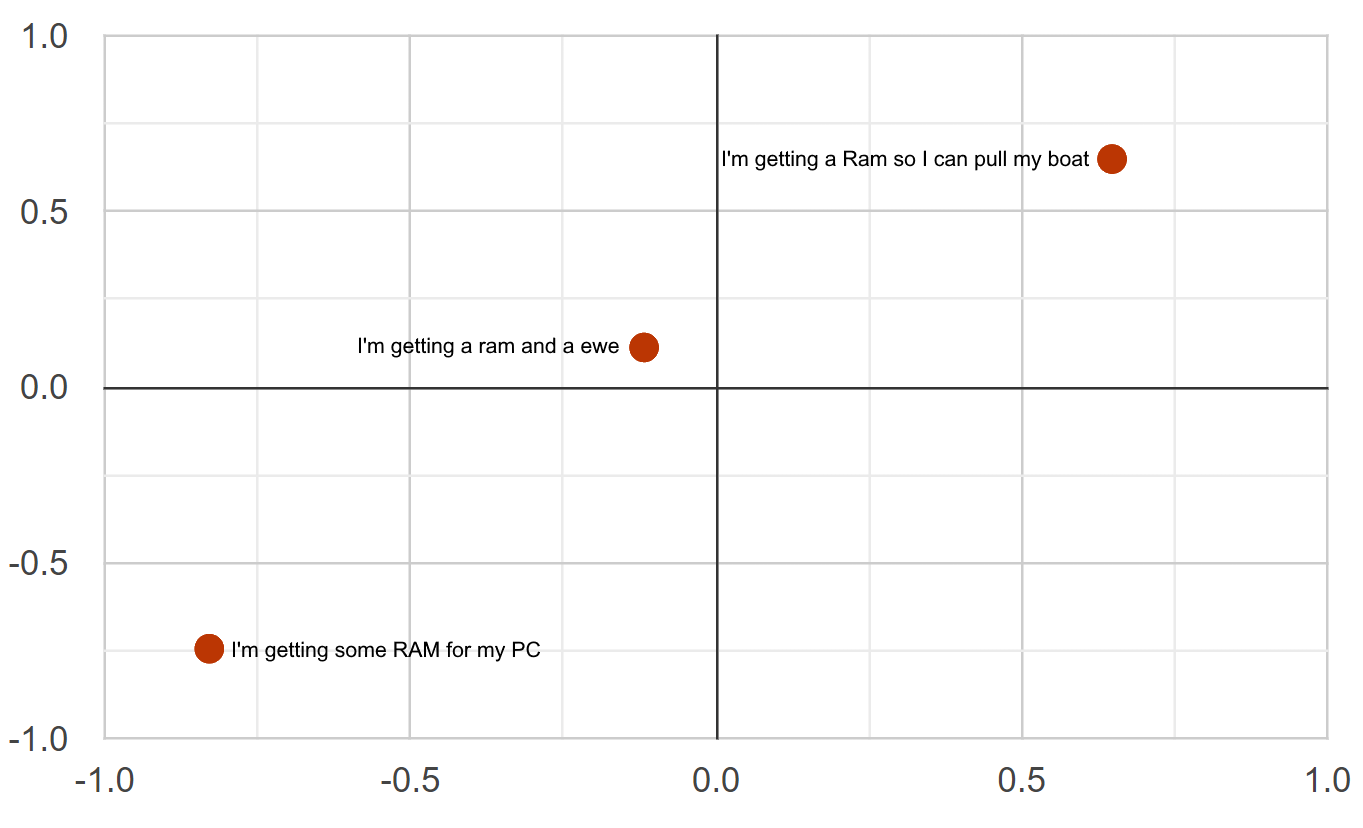
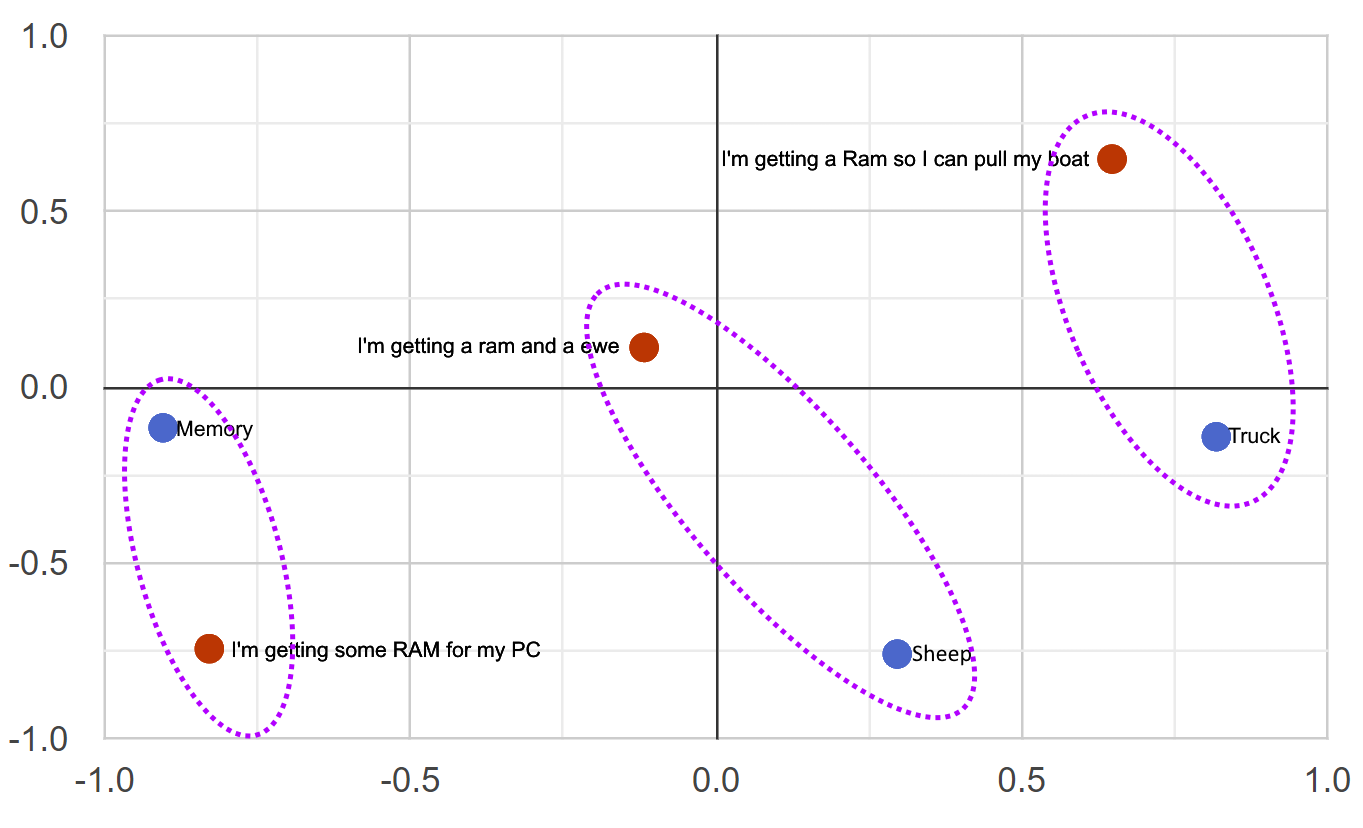
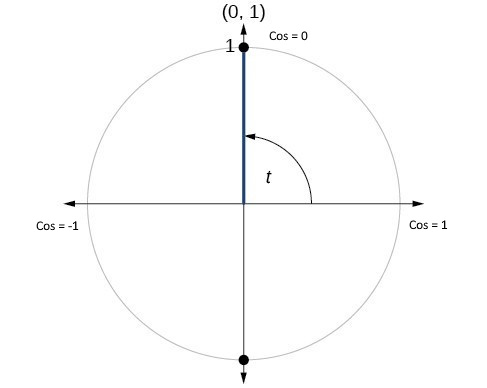
Cosine Similarity & Distance
Note: For normalized vectors, cosine similarity is the same as the dot-product |
|
Cosine Distance
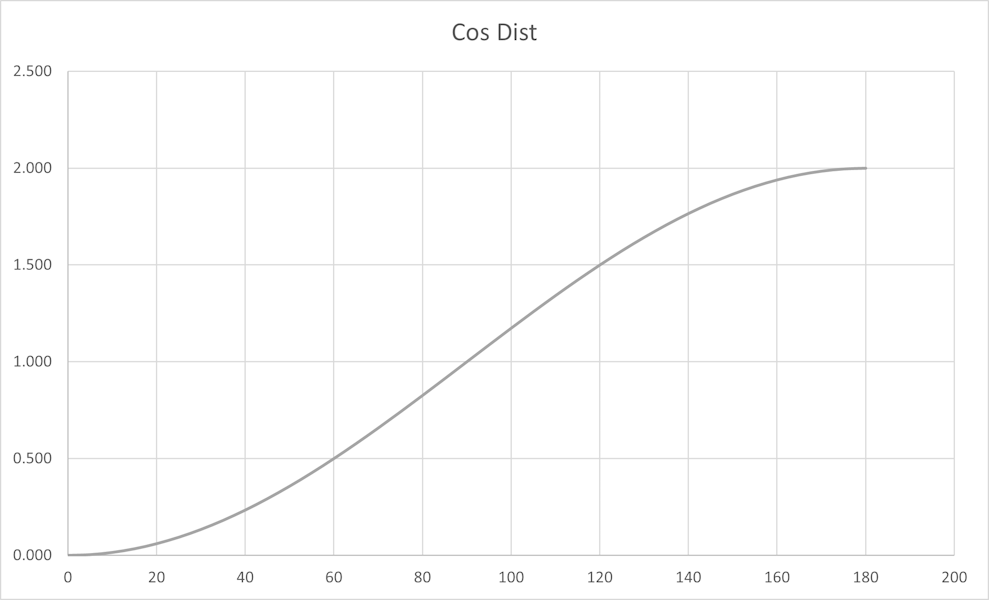
Cosine Distance
Embedding Distance
| Feature | Example |
|---|---|
| Synonym | "Happy" is closer to "Joyful" than to "Sad" |
| Language | "The Queen" is very close to "La Reina" |
| Idiom | "He kicked the bucket" is closer to "He died" than to "He kicked the ball" |
| Sarcasm | "Well, look who's on time" is closer to "Actually Late" than "Actually Early" |
| Homonym | "Bark" (dog sound) is closer to "Howl" than to "Bark" (tree layer) |
| Collocation | "Fast food" is closer to "Junk food" than to "Fast car" |
| Proverb | "The early bird catches the worm" is closer to "Success comes to those who prepare well and put in effort" than to "A bird in the hand is worth two in the bush" |
| Metaphor | "Time is money" is closer to "Don't waste your time" than to "Time flies" |
| Simile | "He is as brave as a lion" is closer to "He is very courageous" than to "He is a lion" |
Modeling Exercise
Design a system to find words/phrases that are far apart (semantically different) in the embedding space?
Assumptions
- No db of embeddings available to search
- Limited understanding of the features of the embedding space
- i.e. changing language changes nearly every dimension
What type of models might work?
- Can we do it logically?
- Can we brute-force it?
- Are there hybrid approaches?
What are the features of each model?
How do we execute the model(s)?

Possible Genes
Categorical
- Part of Speech (noun, verb, etc)
- Register (formal, slang, technical, etc)
- Morphology (root, compound, phrase)
- Animacy (inanimate, animate, agentic, collaborative)
- Scientific Discipline (biology, physical, life/health, etc)
Continuous
- Polarity (negative -> positive)
- Idiomacity (literal -> idiomatic)
- Concreteness (abstract -> concrete)
Other Options
- Language
Mapping Strategies
We need to find what should change in order to identify a word distant from the current one
- Part of Speech: Noun -> Adverb
- Discipline: Software Engineering -> Philosophy
- Polarity: Neutral -> Highly Positive
Linguistic Agent - System Prompt
You are a simulation of a great linguist. You classify words/phrases within the following categories:
- Part of Speech (noun, verb, etc)
- Register (formal, slang, technical, etc)
- Scientific Discipline (biology, physical, life/health, etc)
- Morphology (root, compound, phrase)
- Animacy (inanimate, animate, agentic, collaborative)
- Polarity (highly negative, negative, neutral, positive, highly positive)
- Idiomacity (highly literal, literal, idiomatic, highly idiomatic)
- Concreteness (highly abstract, abstract, concrete, highly concrete)
Your job is to identify words/phrases that meet the requested characteristics. You respond only with the requested word or phrase in lower case.
Linguistic Agent - User Prompt
Give me a word or phrase with the following characteristics:
- Primary part of speech is verb
- Register is technical
- Morphology is phrase
- Animacy is collaborative
- Scientific Discipline is biology
- Polarity is highly negative
- Idiomacity idiomatic
- Concreteness highly concrete
and is not in the following list: "prime genius", "engineer a cooperative symbiosis".
Be sure to only respond with the selected word or phrase, no ceremony.
Commonalities
We discussed 2 problems:
- Game strategy - what's the best move given game state?
- Semantic Distance - what word should I test next?
What do they have in common? What makes them good candidates for genetic algorithms?
Summary
- Genetic Algorithms "Learn" by simulating Darwinian Evolution
- The "DNA" represents the decisions that can be made
- One chromosome per condition (game state)
- One gene per option (choices from a state)
- Several parameters control how solutions evolve
- Simulations per Generation - how often the solutions change
- Fewer simulations make it more likely a less-fit solution will survive over a more-fit solution
- Error (misspelling) rate - how often each chromosome changes between generations
- Higher rates cause greater variations from generation to generation
- Selection strategy - Which solutions survive and mutate
- Survive intact - Remain unchanged to next generation
- Survive mutated - Modified versions survive to next generations
- Survive recombined - Crossover between two solutions survives
- Simulations per Generation - how often the solutions change
Bio-Inspired Algorithms
|

|
Best Path Algorithms
Ant Colony Optimization
Pheromones
|

|
Ant Colony Optimization
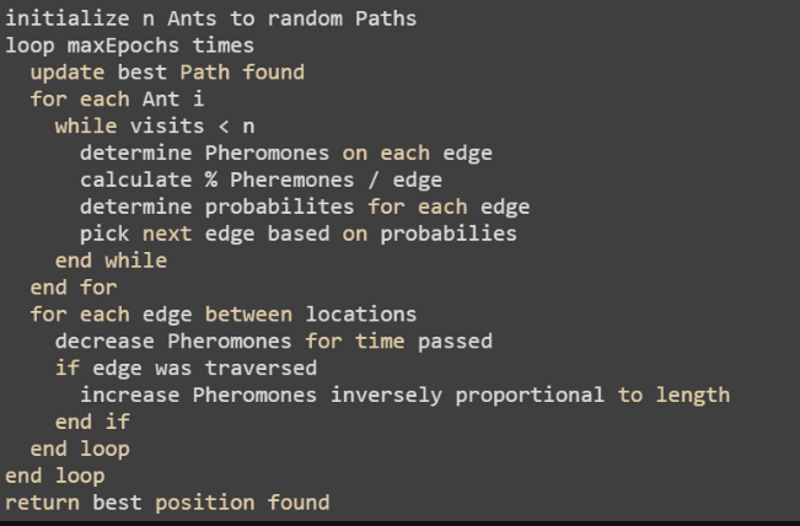
Ant Colony Optimization
|

|
Bee Colony Optimization
Types of Bees
|

|
Bee Colony Optimization
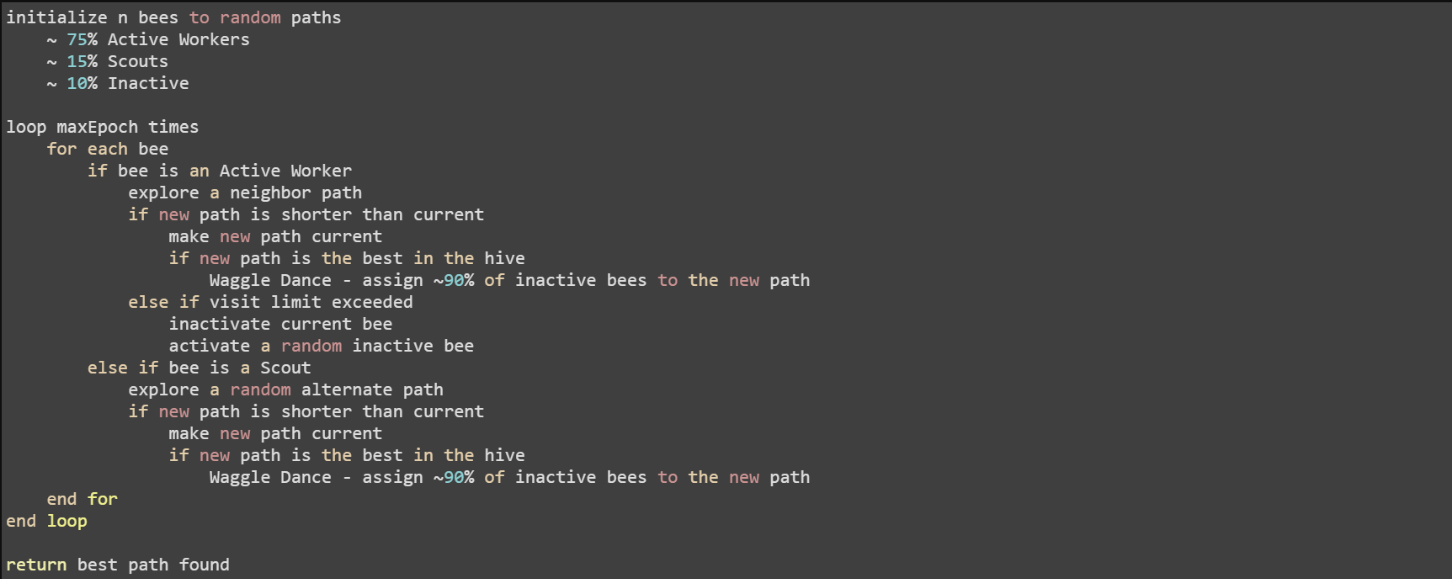
Bee Colony Optimization
|

|
Reducing Costs
Firefly Optimization
initialize n fireflies to random positions
loop maxEpochs times
for each firefly i
for each firefly j
if intensity(i) < intensity(j)
compute attractiveness
move firefly(i) toward firefly(j)
update firefly(i) intensity
end for
end for
sort fireflies
end loop
return best position found
Firefly Optimization
- Neighborhood Search
- Search the area toward best known solution
- Closer and Brighter: More Attractive
- Similar to gravity
- Tweaks
- Number of fireflies
- Range of possible values
- How fast fireflies move
- Features
- Works better for linear problems
- Optimality not guaranteed
- Can suffer from sparseness problems
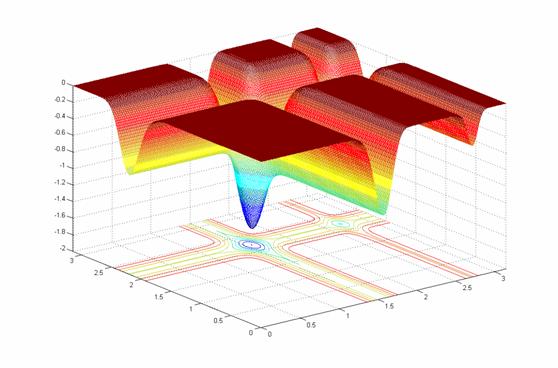
Amoeba Optimization
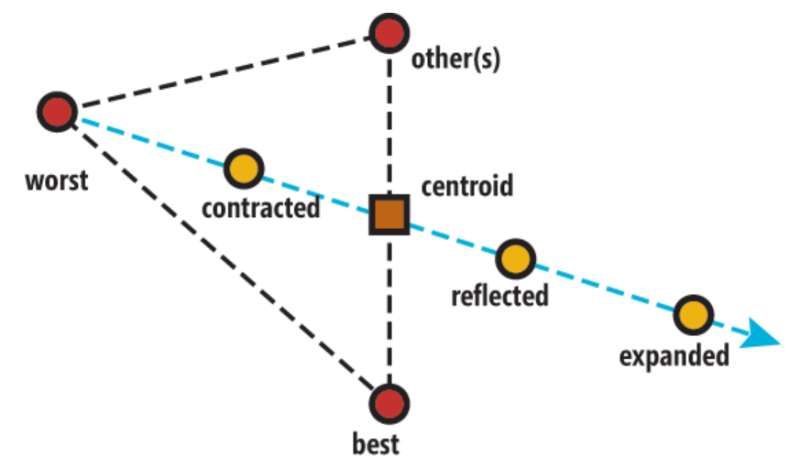
Amoeba Optimization
initialize the amoeba with n (size) locations
loop maxEpochs times
calculate new possible solutions
contracted - midway between centroid and worst
reflected - contracted point reflected across centroid
expanded - beyond reflected point by a constant factor
if any solution is better than the current
replace worst value with best value from new solution
else
shrink (multiple contract) all lesser nodes toward the best
increment epoch count
end loop
return best position found
Amoeba Optimization
- Neighborhood Search
- Start with random locations
- Explore neighbors based on amoeba movement
- Surround the solution, then contract to it
- Tweaks
- Size of the amoeba
- > # of search dimensions
- Number of executions
- Handle local minima
- Size of the amoeba
- Features
- Optimality no guaranteed
- Can suffer from sparseness problems

What Can We Do With This Stuff?
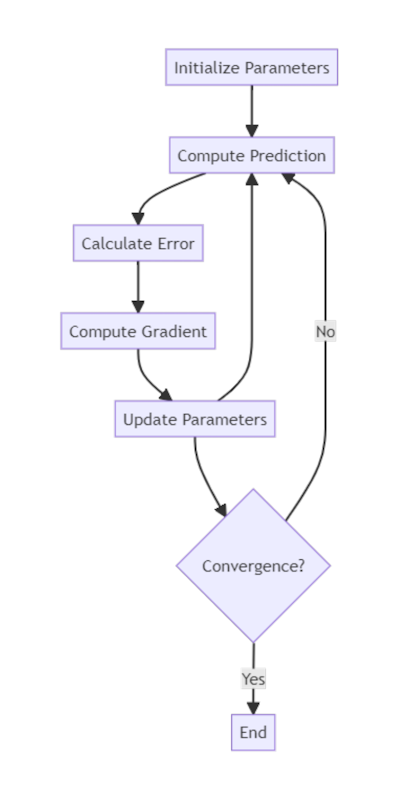
Gradient Descent
|
|
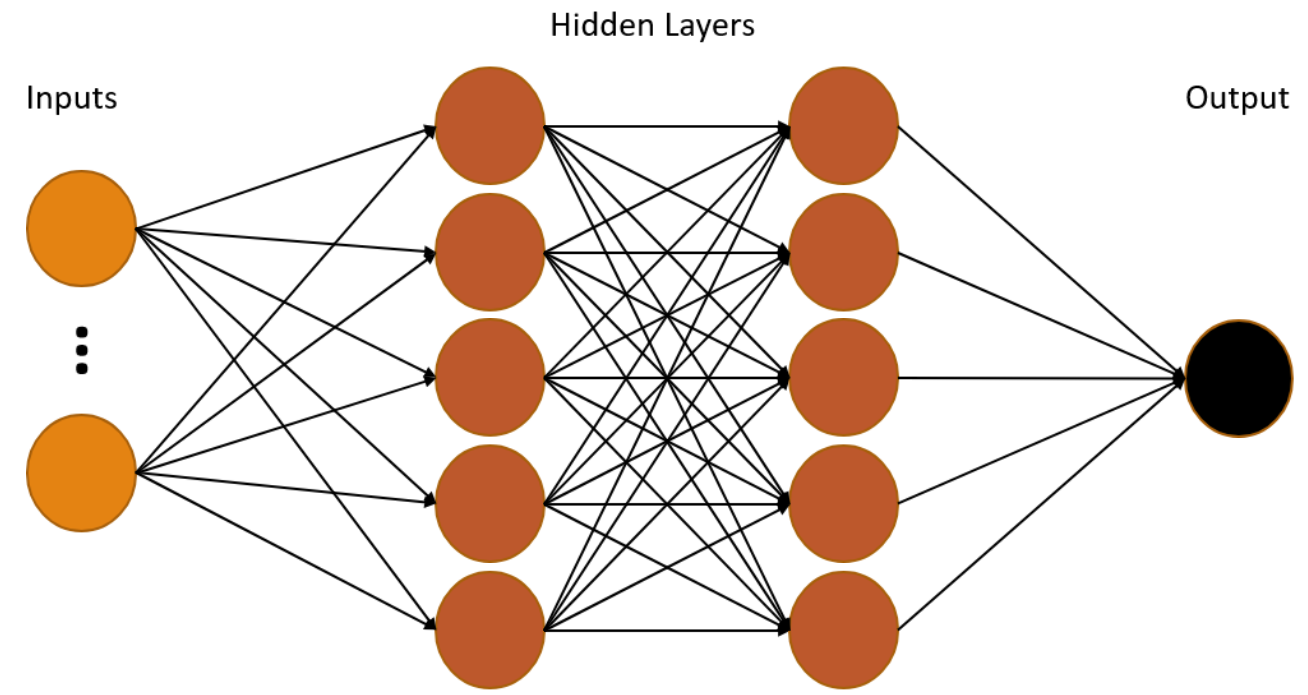
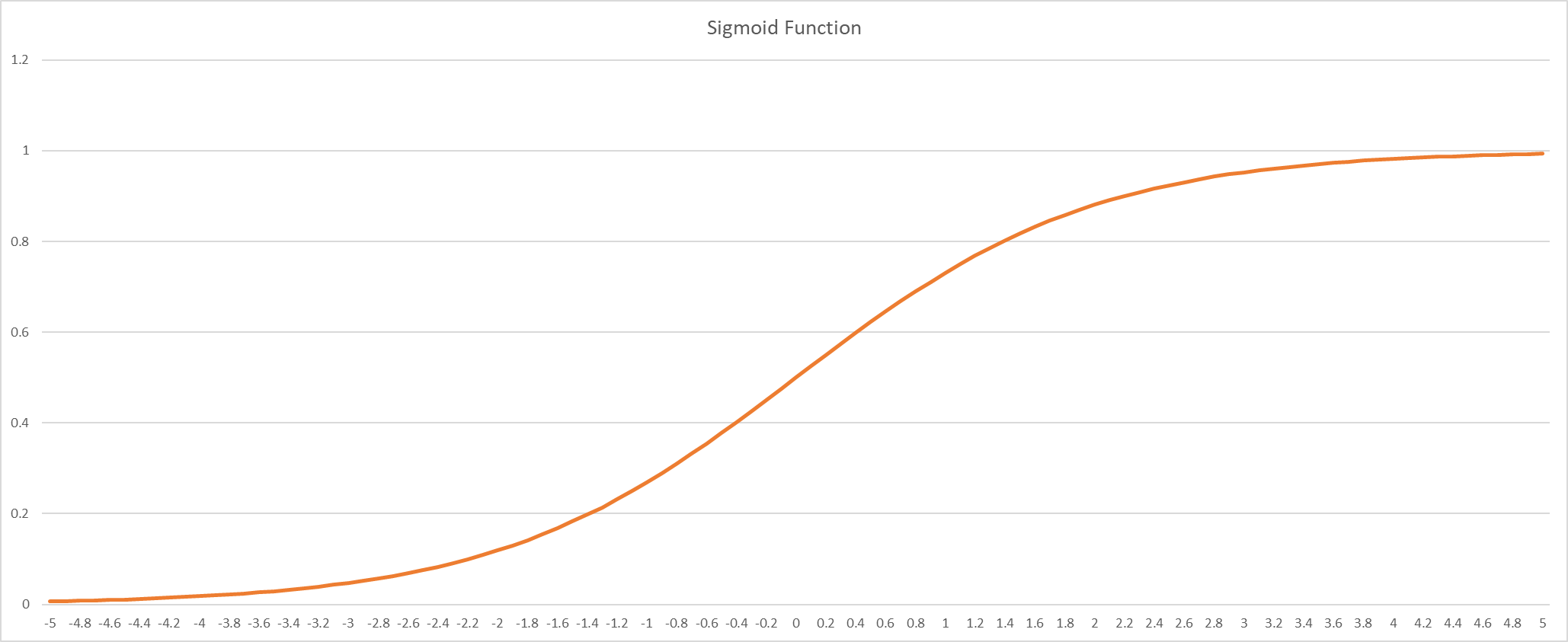
Deep Neural Networks
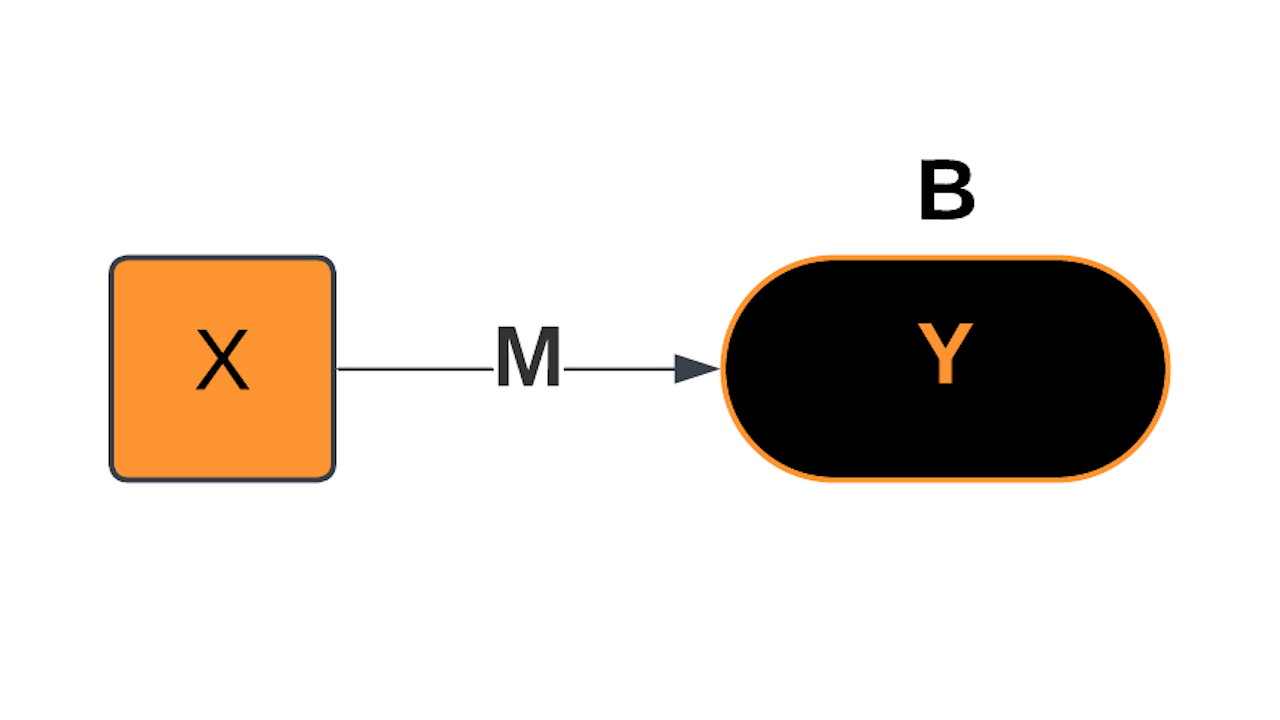
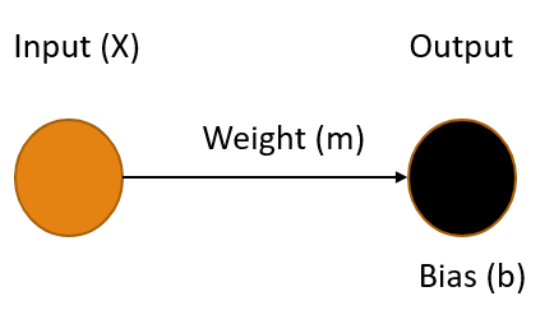
Linear Model
|
|
ML's Linear Linchpin
|
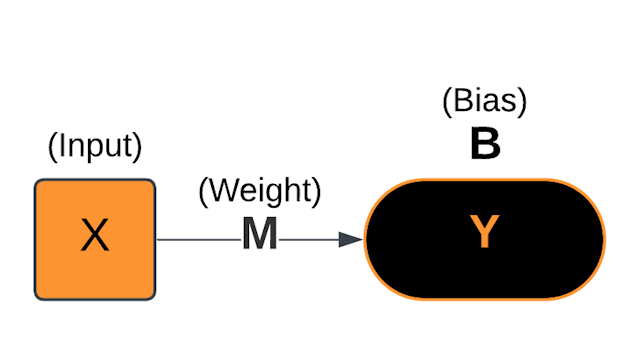
|
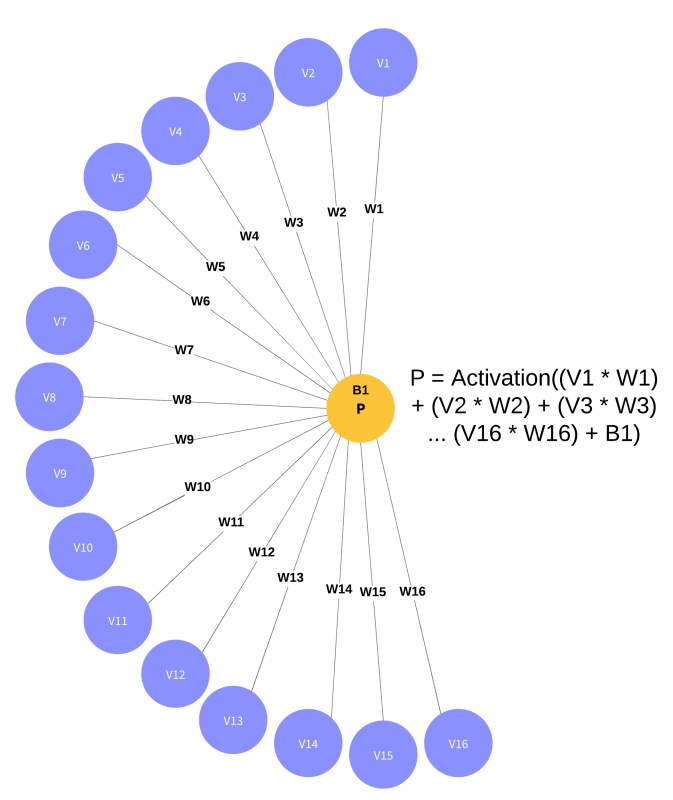
Model Parameters
|
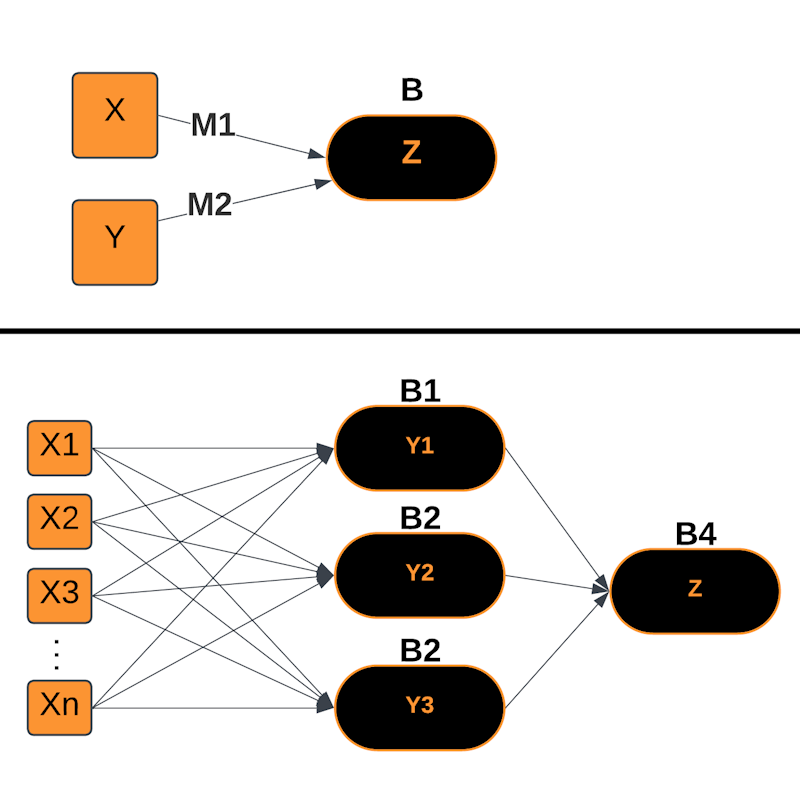
|
Error Function
The weight (m) often has a greater effect on the error than the bias (b) |
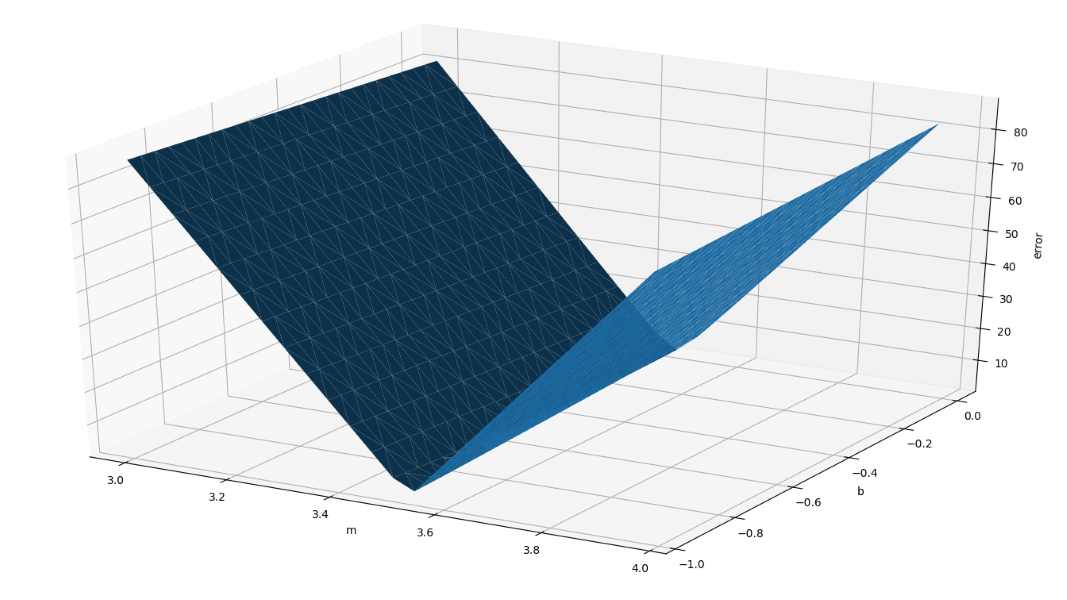
|
Training the Model
|
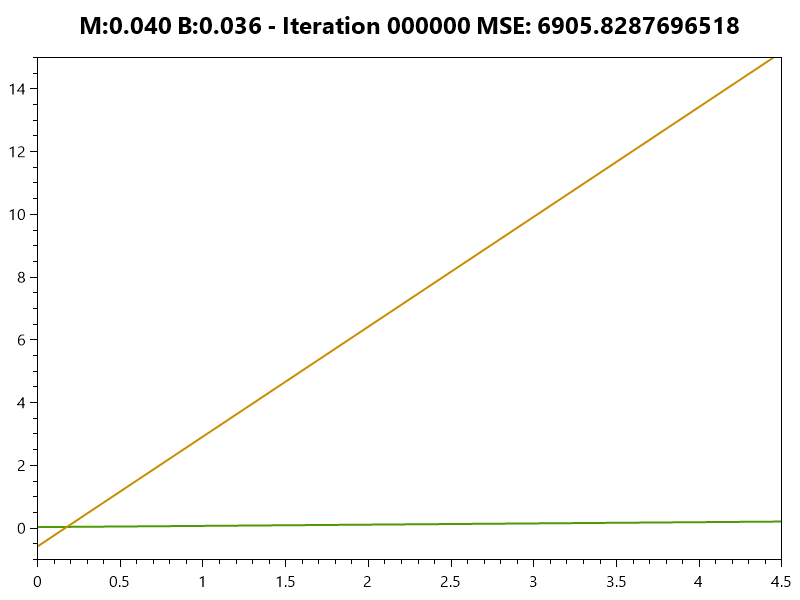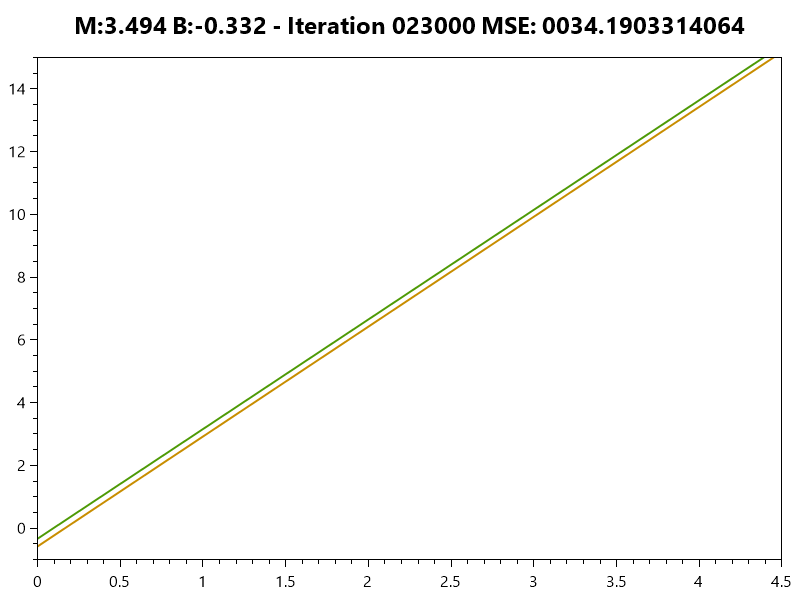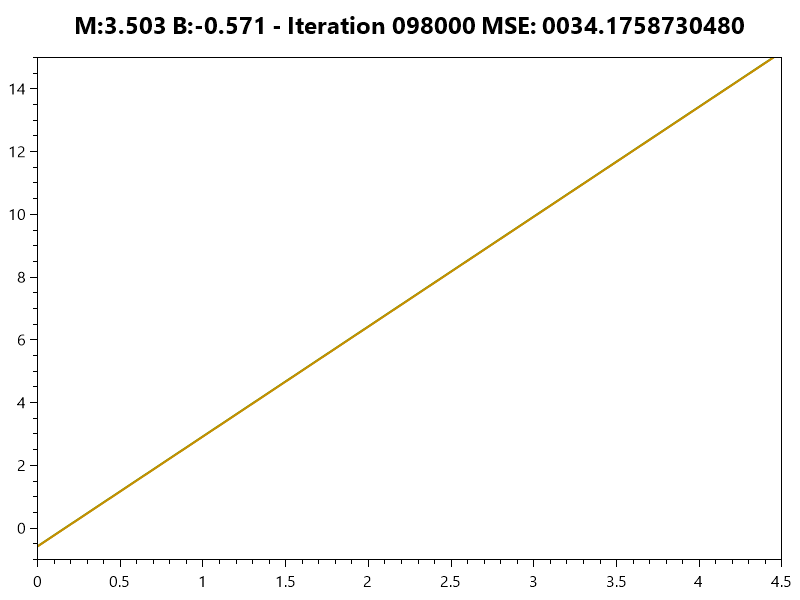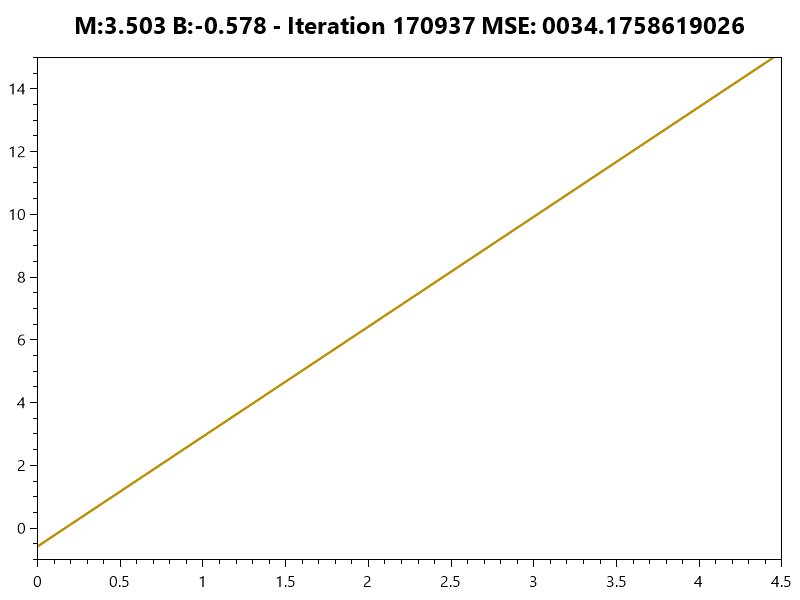
|
Linear Regression Demos

|
Mathematics

...we've invented a fantastic array of tricks and gimmicks for putting together the numbers, without actually doing it. We don't actually [apply Y = Mx+B for every neuron] We do it by the tricks of mathematics, and that's all. So, we're not going to worry about that. You don't have to know about [Linear Algebra]. All you have to know is what it is, tricky ways of doing something which would be laborious otherwise.
With apologies to Professor Feynman, who was talking about the tricks of Calculus as applied to Physics, not the tricks of Linear Algebra as applied to Machine Learning.
Railroad Times Model

Linear Regression Model
Predict the unknown values in a linear equation
|
|
Voter Model
ML Demo
Using Amoeba Optimzation to Train an ML Model
More Bio-Inspired
|

|
Solving Tractable Problems
Understand the Problem Deeply
Clarify inputs, outputs, constraints, and goals
Is optimality required? Can constraints be relaxed?
Identify if it can be broken into reusable parts?
Classify the Problem Type
Search? Optimization? Graph traversal? Dynamic programming candidate?
Are brute-force or exponential-time solutions feasible?
What tools do we have that can help? Can we buy vs build?
Implement and Test
Try a naive solution 1st
Use test cases to validate correctness and performance
Optimize as needed / Start over if necessary
Resources - Page 1
|

|
Resources - Page 2

|
Solving Your Problems
|
Would you like to try to model a problem from one of your domains? |
Bonus Content
Linear Programming (LP) & Mixed-Integer Programming (MIP)
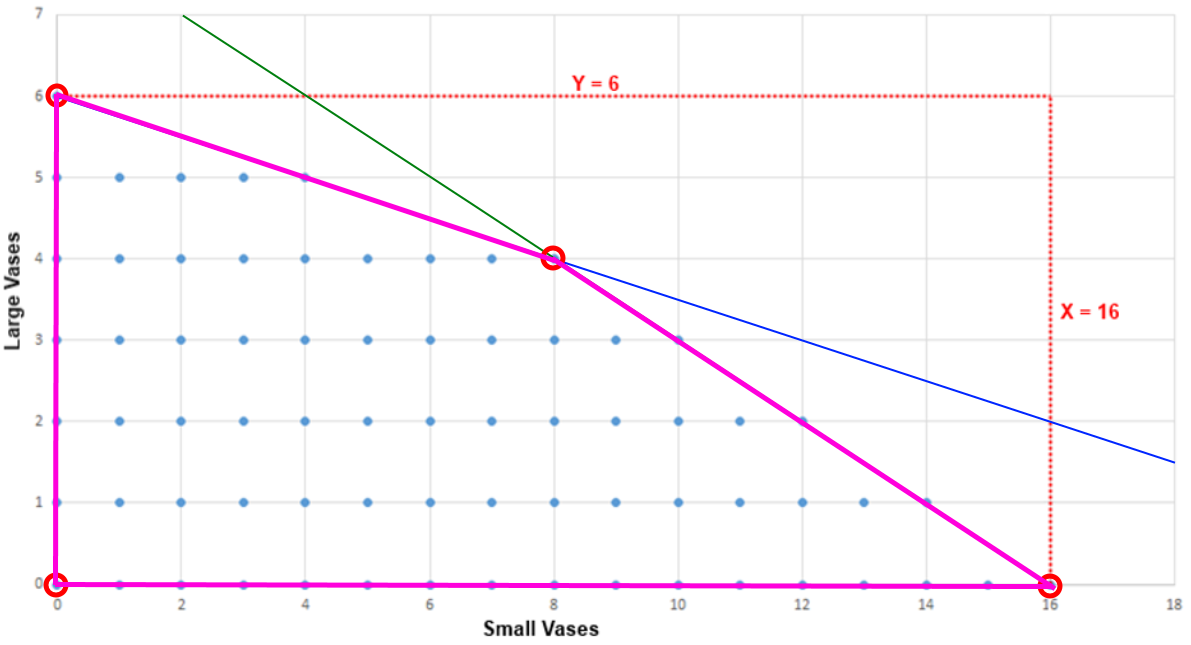
Use Case: Production Targets
|
|
|
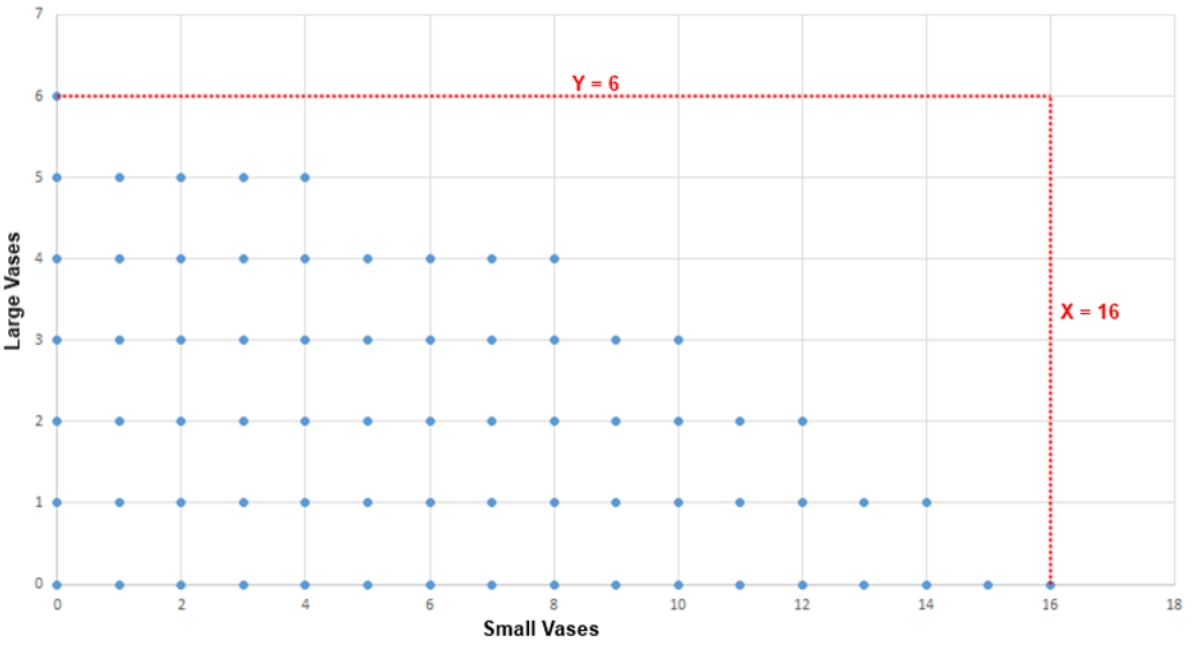
Solution Space
Constraint Equations
- Clay Constraint
- X + 4Y <= 24
- X <= 24 and Y <= 6
- X + 4Y <= 24
- Glaze Constraint
- X + 2Y <= 16
- X <=16 and Y <= 8
- X + 2Y <= 16
Feasible Region
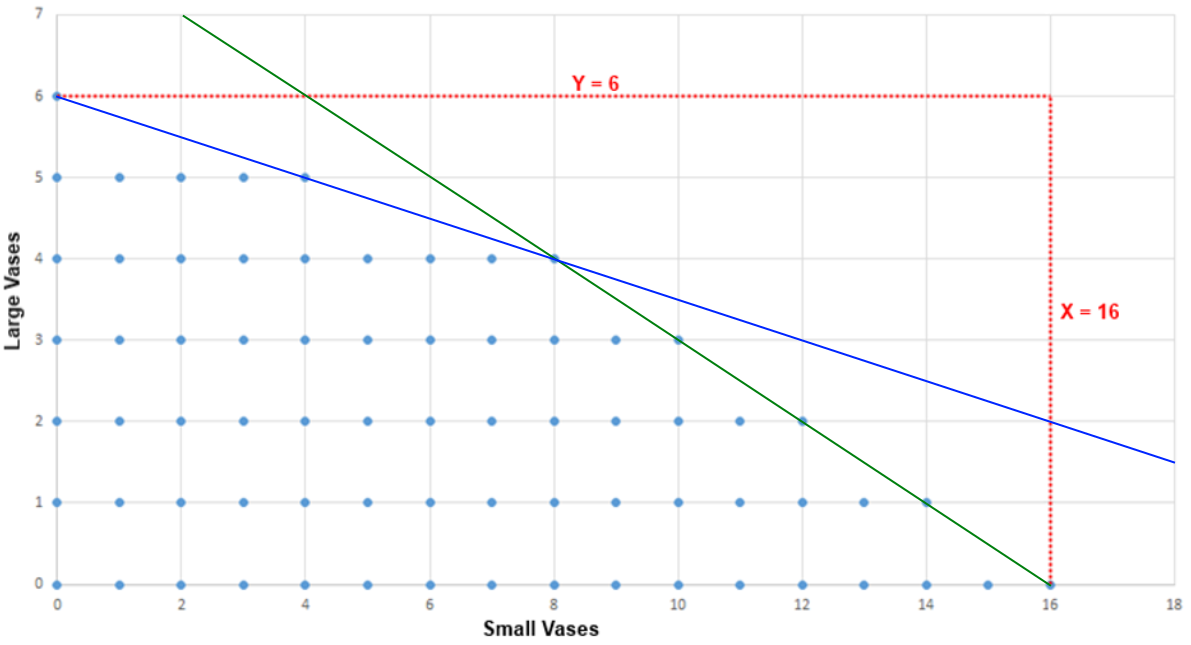
Linear Programming - Polytope
Linear and Mixed-Integer Programming
|
|
Search/Optimization Models
George Dantzig - Creator of the Simplex Algorithm